/Szkoła średnia/Geometria/Stereometria/Walec

Zadanie nr 8466615

Dodaj do ulubionych
Dodaj do rozwiązanych

W stożek o promieniu podstawy długości 6 wpisano walec, w ten sposób, że jedna podstawa walca zawiera się w podstawie stożka, a brzeg jego drugiej podstawy zawiera się w powierzchni bocznej stożka. Oblicz promień podstawy walca, jeżeli jego objętość stanowi 4 9 objętości stożka.

Rozwiązanie

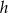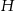Rysujemy przekrój osiowy stożka i oznaczmy przez h i r wysokość i promień walca, a przez H wysokość stożka.

PIC

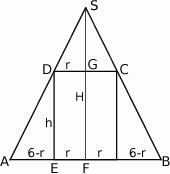
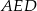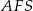Zauważmy, że trójkąty AED i AF S są podobne. Korzystając z tego podobieństwa mamy

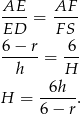
AE--= AF-- ED FS 6− r 6 -----= -- h H H = -6h--. 6− r

Zapiszmy teraz informację o wzajemnej objętości obu figur.

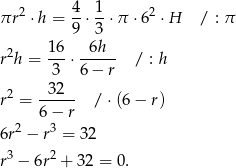
4 1 πr2 ⋅h = -⋅ --⋅π ⋅62 ⋅H / : π 9 3 2 1-6 -6h-- r h = 3 ⋅ 6− r / : h 3 2 r2 = ----- /⋅ (6− r) 6 − r 6r2 − r3 = 32 3 2 r − 6r + 3 2 = 0.

Musimy teraz rozwiązać to równanie. Szukamy pierwiastków wymiernych. Sprawdzając dzielniki wyrazu wolnego można znaleźć pierwiastek 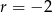r = − 2 . Dzielimy wielomian przez 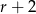r + 2 , my zrobimy to grupując wyrazy.

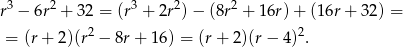
3 2 3 2 2 r − 6r + 32 = (r + 2r ) − (8r + 16r)+ (16r+ 32) = = (r+ 2)(r2 − 8r + 16) = (r + 2)(r − 4)2.

Zatem jedyny dodatni pierwiastek tego równania to 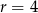r = 4 .  
Odpowiedź: 4

Wersja PDF