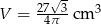Zadanie nr 9619937
Powierzchnia boczna walca po rozwinięciu jest prostokątem, którego przekątna ma długość 6 cm i tworzy z bokiem odpowiadającym wysokości walca kąt o mierze 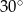 . Oblicz objętość walca.
. Oblicz objętość walca.
Rozwiązanie
Zaczynamy od szkicowego rysunku.
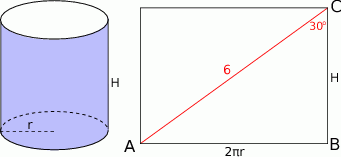
Po rozwinięciu powierzchni bocznej walca, otrzymamy prostokąt o bokach długości 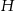 i
i 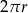 , gdzie
, gdzie  jest promieniem podstawy walca. Patrząc na trójkąt
jest promieniem podstawy walca. Patrząc na trójkąt 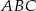 mamy
mamy
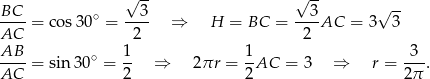
Liczymy teraz objętość walca.
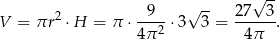
Odpowiedź: