/Szkoła średnia/Geometria/Stereometria/Ostrosłup/Prawidłowy czworokątny

Zadanie nr 2403582

Dodaj do ulubionych
Dodaj do rozwiązanych

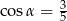W ostrosłupie prawidłowym czworokątnym ściana boczna jest nachylona do płaszczyzny podstawy pod kątem ostrym α , dla którego co sα = 35 . Wysokość ostrosłupa ma długość 12 cm. Oblicz objętość tego ostrosłupa.

Rozwiązanie

Zaczynamy od rysunku

PIC

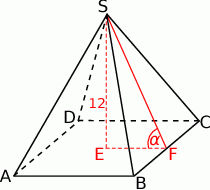
Obliczmy 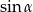sin α z jedynki trygonometrycznej.

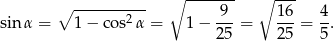
∘ ---------- ∘ ------- ∘ --- 2 9-- 16- 4- sinα = 1 − cos α = 1− 25 = 25 = 5.

To pozwala obliczyć długość odcinka 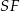SF .

4-= sin α = SE- = -12 ⇒ SF = 12 ⋅ 5-= 15. 5 SF SF 4

Z twierdzenia Pitagorasa w trójkącie 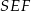SEF obliczamy EF .

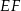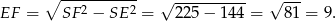
∘ ----------- √ ---------- √ --- EF = SF 2 − SE 2 = 225 − 144 = 81 = 9.

W takim razie 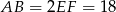AB = 2EF = 18 i objętość ostrosłupa jest równa:

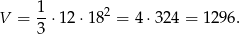
V = 1⋅ 12⋅ 182 = 4 ⋅324 = 12 96. 3

 
Odpowiedź: 129 6 cm 3

Wersja PDF