/Szkoła średnia/Geometria/Stereometria/Ostrosłup/Prawidłowy czworokątny

Zadanie nr 3026333

Dodaj do ulubionych
Dodaj do rozwiązanych

W ostrosłupie prawidłowym czworokątnym krawędź boczna tworzy z krawędzią podstawy kąta α . Wyznacz cosinus kąta między sąsiednimi ścianami bocznymi.

Rozwiązanie

Zaczynamy oczywiście od rysunku.

PIC

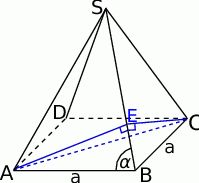
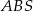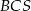Musimy na początek ustalić, jak zaznaczyć interesujący nas kąt między sąsiednimi ścianami bocznymi. Ponieważ trójkąty w ścianach bocznych są przystające, gdy opuścimy wysokości w trójkątach ABS i BCS na krawędź 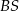BS to przetną one tę krawędź w tym samym punkcie 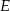E . I mamy to, o co nam chodziło: płaszczyzna 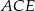ACE jest teraz prostopadła do krawędzi 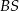BS , zatem interesujący nas kąt to kąt przy wierzchołku 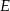E w trójkącie AEC .

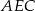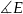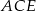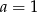Aby wyliczyć kosinus kąta ∡E , możemy skorzystać z twierdzenia cosinusów w trójkącie ACE . Zanim to jednak zrobimy, wyliczmy boki tego trójkąta. Przyjmijmy, że krawędź podstawy ma długość a (równie dobrze możemy wziąć a = 1 , nie ma to żadnego znaczenia). Z trójkąta prostokątnego 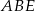ABE mamy

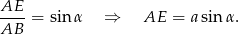
AE-- AB = sin α ⇒ AE = asin α.

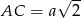Ponadto √ -- AC = a 2 , więc możemy napisać twierdzenie cosinusów.

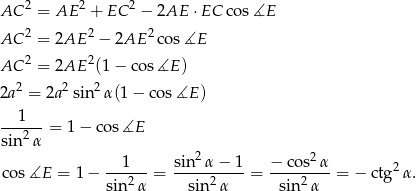
2 2 2 AC = AE + EC − 2AE ⋅EC co s∡E AC 2 = 2AE 2 − 2AE 2cos ∡E AC 2 = 2AE 2(1 − co s∡E ) 2 2 2 2a = 2a sin α(1 − cos ∡E ) 1 ---2--= 1− cos∡E sin α 2 2 --1--- sin--α−--1 −--cos-α- 2 cos ∡E = 1− sin2α = sin2 α = sin 2α = − ctg α.

To, że cosinus wyszedł ujemny, to nic dziwnego – po prostu kąt 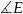∡E jest zawsze rozwarty.  
Odpowiedź: 2 − ctg α

Wersja PDF