/Szkoła średnia/Geometria/Stereometria/Ostrosłup/Prawidłowy czworokątny

Zadanie nr 3717304

Dodaj do ulubionych
Dodaj do rozwiązanych

W ostrosłup prawidłowy czworokątny wpisano sześcian tak, że jego cztery wierzchołki należą do wysokości ścian bocznych ostrosłupa, a pozostałe do płaszczyzny podstawy. Oblicz stosunek objętości ostrosłupa do objętości sześcianu jeżeli kąt nachylenia ściany bocznej do płaszczyzny podstawy jest równy α .

Rozwiązanie

Oznaczmy przez a długość krawędzi podstawy ostrosłupa, a przez x długość krawędzi sześcianu.

PIC

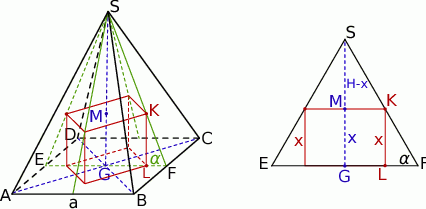
Z trójkąta prostokątnego 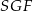SGF obliczamy wysokość ostrosłupa

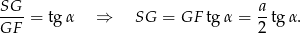
-SG-= tgα ⇒ SG = GF tg α = atg α. GF 2

Zauważmy jeszcze, że

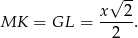
√ -- MK = GL = x--2-. 2

Sposób I

Patrzymy na trójkąt prostokątny 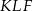KLF .

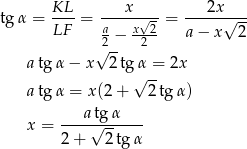
KL-- ---x---- ---2x---- tgα = LF = a x√-2 = √ -- √2-− 2 a − x 2 atg α− x 2tg α = 2x √ -- atg α = x(2 + 2 tgα) a tgα x = ----√------- 2 + 2 tgα

Możemy teraz obliczyć interesujący nas stosunek objętości

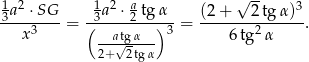
√ -- 13a2-⋅SG-- -13a2 ⋅-a2 tg-α (2-+---2-tgα)3- x3 = ( atgα ) 3 = 6 tg2α . 2+-√2tgα

Sposób II

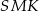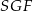Tym razem korzystamy z podobieństwa trójkątów SMK i SGF . Mamy zatem

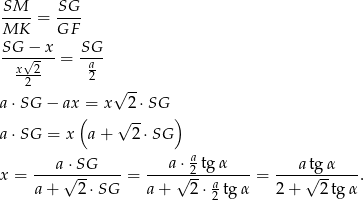
SM-- SG-- MK = GF SG − x SG ---√----= -a-- x2-2 2 √ -- a ⋅SG − ax = x 2⋅SG ( √ -- ) a ⋅SG = x a + 2 ⋅SG a⋅SG a ⋅ a tg α atg α x = ----√-------= ----√-2--------= ----√------. a+ 2⋅SG a + 2 ⋅ a2 tg α 2+ 2tg α

Stosunek objętości obliczamy tak samo jak w poprzednim sposobie.  
Odpowiedź: - (2+√-2tgα)3 6tg2α

Wersja PDF