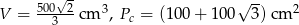Zadanie nr 4643983
Podstawą ostrosłupa prawidłowego jest kwadrat o przekątnej 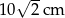 . Krawędź boczna ostrosłupa tworzy z podstawą kąt o mierze
. Krawędź boczna ostrosłupa tworzy z podstawą kąt o mierze 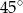 . Oblicz pole powierzchni całkowitej i objętość tego ostrosłupa.
. Oblicz pole powierzchni całkowitej i objętość tego ostrosłupa.
Rozwiązanie
Zaczynamy od rysunku.
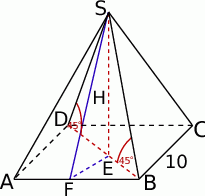
Ponieważ przekątna kwadratu o boku  ma długość
ma długość 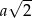 , mamy
, mamy
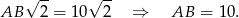
Łatwo wyliczyć długość wysokości 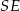 ostrosłupa. Można to zrobić na różne sposoby: można zauważyć, że trójkąt
ostrosłupa. Można to zrobić na różne sposoby: można zauważyć, że trójkąt 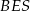 jest równoramienny (dwa kąty mają miarę
jest równoramienny (dwa kąty mają miarę 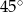 ); można zauważyć, że trójkąt
); można zauważyć, że trójkąt 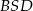 jest połówką kwadratu, czyli
jest połówką kwadratu, czyli 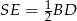 ; można wreszcie skorzystać wprost z definicji funkcji trygonometrycznych w trójkącie
; można wreszcie skorzystać wprost z definicji funkcji trygonometrycznych w trójkącie 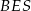 . Tak czy inaczej otrzymamy
. Tak czy inaczej otrzymamy
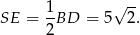
Możemy teraz policzyć objętość
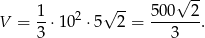
Aby policzyć pole powierzchni całkowitej, wyliczmy najpierw wysokość 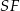 trójkąta
trójkąta 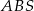 . Patrzymy na trójkąt
. Patrzymy na trójkąt 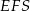 .
.
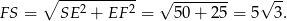
Liczymy teraz pole powierzchni całkowitej
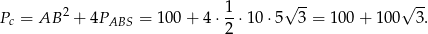
Odpowiedź: