Zadanie nr 5440384
Dany jest ostrosłup prawidłowy czworokątny o wysokości 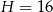 . Suma długości wszystkich jego krawędzi jest równa
. Suma długości wszystkich jego krawędzi jest równa 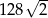 . Oblicz cosinus kąta nachylenia ściany bocznej do płaszczyzny podstawy tego ostrosłupa.
. Oblicz cosinus kąta nachylenia ściany bocznej do płaszczyzny podstawy tego ostrosłupa.
Rozwiązanie
Rozpoczynamy od rysunku.
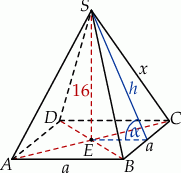
Oznaczmy przez  długość krawędzi podstawy ostrosłupa i przez
długość krawędzi podstawy ostrosłupa i przez  długość jego krawędzi bocznej. Mamy zatem
długość jego krawędzi bocznej. Mamy zatem
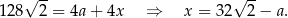
Korzystając ze wzoru na długość przekątnej kwadratu mamy
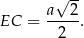
Piszemy teraz twierdzenie Pitagorasa w trójkącie prostokątnym  .
.
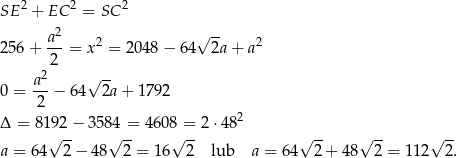
Druga odpowiedź prowadzi jednak do sprzeczności, bo wtedy 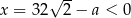 . Mamy zatem
. Mamy zatem 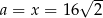 .
.
Liczymy teraz wysokość ściany bocznej
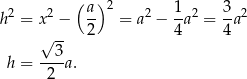
Stąd
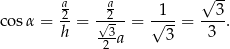
Odpowiedź: