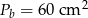/Szkoła średnia/Geometria/Stereometria/Ostrosłup/Prawidłowy czworokątny

Zadanie nr 7215822

Dodaj do ulubionych
Dodaj do rozwiązanych

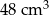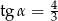Dany jest ostrosłup prawidłowy czworokątny o objętości 3 4 8 cm . Ściana boczna jest nachylona do podstawy pod takim kątem α , że tg α = 43 . Wyznacz pole powierzchni bocznej tego ostrosłupa.

Rozwiązanie

Zaczynamy od rysunku

PIC

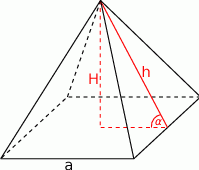
Z założeń otrzymujemy układ równań

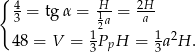
{ 4 H 2H 3 = tg α = 1a = -a- 12 1 2 48 = V = 3PpH = 3a H .

Wyznaczamy z pierwszego równania a

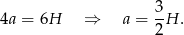
4a = 6H ⇒ a = 3H . 2

Podstawiamy do drugiego równania

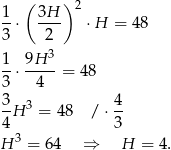
( ) 2 1-⋅ 3H-- ⋅H = 48 3 2 1 9H 3 --⋅ -----= 48 3 4 3- 3 4- 4 H = 48 /⋅ 3 3 H = 6 4 ⇒ H = 4.

Zatem

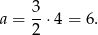
3 a = --⋅4 = 6. 2

Z twierdzenia Pitagorasa obliczamy wysokość ściany bocznej

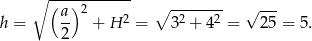
∘ (--)-2------ ∘ ------- √ --- h = a- + H2 = 32 + 42 = 25 = 5. 2

Teraz już łatwo policzyć pole boczne

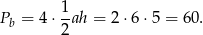
Pb = 4 ⋅ 1-ah = 2 ⋅6 ⋅5 = 60. 2

 
Odpowiedź: Pb = 60 cm 2

Wersja PDF