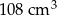Zadanie nr 7934657
Wysokość ostrosłupa prawidłowego czworokątnego tworzy ze ścianą boczną kąt o mierze 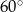 . Pole powierzchni bocznej ostrosłupa jest równe
. Pole powierzchni bocznej ostrosłupa jest równe 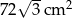 . Oblicz objętość ostrosłupa.
. Oblicz objętość ostrosłupa.
Rozwiązanie
Rozpoczynamy od szkicowego rysunku.
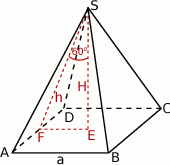
Oznaczmy przez  długość krawędzi podstawy ostrosłupa, przez
długość krawędzi podstawy ostrosłupa, przez 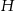 długość jego wysokości, a przez
długość jego wysokości, a przez 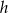 długość wysokości ściany bocznej.
długość wysokości ściany bocznej.
Z trójkąta 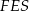 mamy
mamy
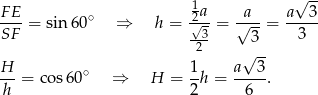
Pole ściany bocznej jest równe 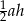 , więc wiemy, że
, więc wiemy, że
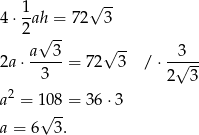
Liczymy objętość ostrosłupa
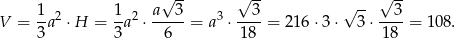
Odpowiedź: