Zadanie nr 2709997
Podstawy trapezu 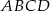 mają długości
mają długości 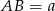 i
i 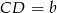 . Na ramionach trapezu wybrano punkty
. Na ramionach trapezu wybrano punkty 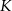 i
i 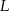 w ten sposób, że odcinek
w ten sposób, że odcinek 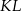 jest równoległy do podstaw i dzieli trapez na dwa trapezy o równych polach. Oblicz długość odcinka
jest równoległy do podstaw i dzieli trapez na dwa trapezy o równych polach. Oblicz długość odcinka 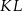 .
.
Rozwiązanie
Niech 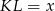 i oznaczmy wysokości trapezów
i oznaczmy wysokości trapezów 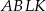 i
i 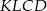 przez
przez 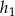 i
i 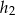 odpowiednio.
odpowiednio.
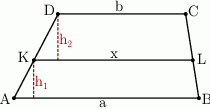
Zapiszmy fakt, że pola dwóch utworzonych trapezów stanowią połowę pola trapezu 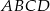
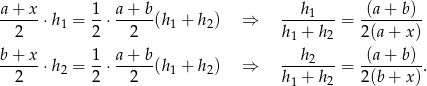
Dodajemy dwie powyższe równości stronami i mamy
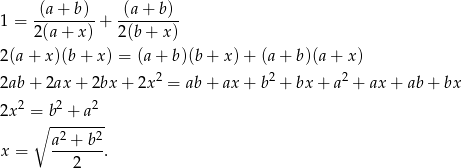
Odpowiedź: