Zadanie nr 4750074
Oblicz pole trapezu, którego podstawy mają długości 2 i 3, a przekątne długości 3 i 4.
Rozwiązanie
Szkicujemy trapez.
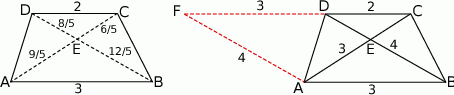
Sposób I
Jedną z podstawowych własności trapezu, jest podobieństwo trójkątów 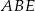 i
i 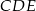 (tak jest bo mają takie same kąty). W dodatku skala podobieństwa wynosi
(tak jest bo mają takie same kąty). W dodatku skala podobieństwa wynosi 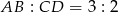 . Znając długości przekątnych, możemy więc wyliczyć długości odcinków na jakie dzieli przekątne ich punkt przecięcia
. Znając długości przekątnych, możemy więc wyliczyć długości odcinków na jakie dzieli przekątne ich punkt przecięcia  .
.
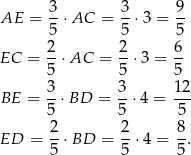
Ogólnie, gdybyśmy chcieli teraz policzyć pole trapezu, czyli pola czterech trójkątów na które dzielą go przekątne, to powinniśmy wyliczyć (np. z twierdzenia cosinusów) 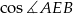 i potem wyliczyć z niego sinus, a na koniec policzyć pola trójkątów ze wzoru z sinusem. W tym przykładzie sytuacja jest jednak wyjątkowo prosta, bo okazuje się, że kąta
i potem wyliczyć z niego sinus, a na koniec policzyć pola trójkątów ze wzoru z sinusem. W tym przykładzie sytuacja jest jednak wyjątkowo prosta, bo okazuje się, że kąta 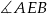 jest prosty (gdybyśmy tego nie zauważyli, to wyszłoby to z twierdzenia cosinusów). Sprawdźmy, że tak jest istotnie (twierdzenie odwrotne do twierdzenia Pitagorasa).
jest prosty (gdybyśmy tego nie zauważyli, to wyszłoby to z twierdzenia cosinusów). Sprawdźmy, że tak jest istotnie (twierdzenie odwrotne do twierdzenia Pitagorasa).
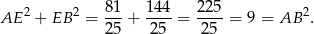
Skoro wszystkie cztery trójkąty są prostokątne i znamy długości ich przyprostokątnych, bez trudu liczymy ich pola.
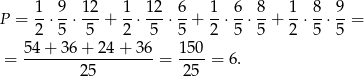
Sposób II
Niech 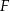 będzie takim punktem półprostej
będzie takim punktem półprostej 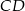 , że
, że 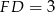 . Wtedy czworokąt
. Wtedy czworokąt 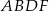 jest równoległobokiem, więc
jest równoległobokiem, więc 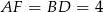 . To oznacza, że trójkąt
. To oznacza, że trójkąt 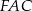 jest trójkątem o bokach 3, 4, 5, jest to więc trójkąt prostokątny o polu
jest trójkątem o bokach 3, 4, 5, jest to więc trójkąt prostokątny o polu
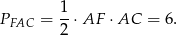
Zauważmy teraz, że
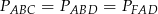
(tak jest, bo każdy z tych trójkątów ma podstawę długości 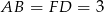 i wysokość równą odległości między prostymi
i wysokość równą odległości między prostymi 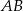 i
i 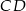 ). W takim razie
). W takim razie
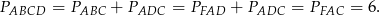
Sposób III
Niech 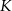 i
i 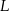 będą rzutami punktów
będą rzutami punktów 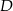 i
i 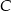 na podstawę
na podstawę 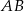 oraz niech
oraz niech 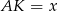 .
.
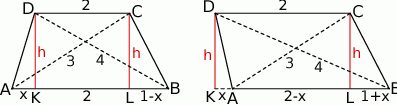
Wtedy
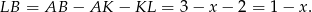
Piszemy teraz twierdzenia Pitagorasa w trójkątach 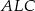 i
i 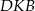 .
.
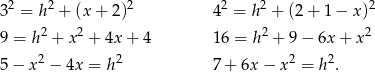
Porównujemy teraz wartości 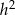 z obu równań i mamy
z obu równań i mamy
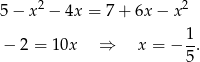
Otrzymaliśmy ujemną wartość  , co w pierwszej chwili może wyglądać dziwnie, ale jak chwilę się zastanowimy, to nie jest trudno ustalić dlaczego tak się stało. Powód jest prosty: nasz rysunek był zły – ujemna wartość
, co w pierwszej chwili może wyglądać dziwnie, ale jak chwilę się zastanowimy, to nie jest trudno ustalić dlaczego tak się stało. Powód jest prosty: nasz rysunek był zły – ujemna wartość  wskazuje na to, że punkt
wskazuje na to, że punkt 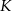 powinien być na lewo od
powinien być na lewo od 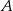 , a nie na prawo (prawy rysunek). Spróbujmy powtórzyć powyższy rachunek, ale używając prawego rysunku. Zauważmy najpierw, że
, a nie na prawo (prawy rysunek). Spróbujmy powtórzyć powyższy rachunek, ale używając prawego rysunku. Zauważmy najpierw, że 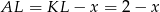 oraz
oraz 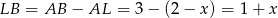 . Piszemy twierdzenia Pitagorasa.
. Piszemy twierdzenia Pitagorasa.
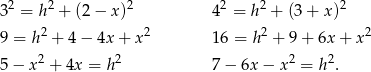
Porównujemy teraz wartości 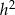 z obu równań i mamy
z obu równań i mamy
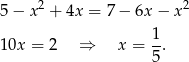
Obliczamy teraz wysokość trapezu.
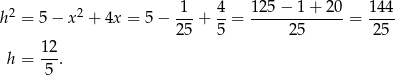
Pole trapezu jest więc równe.
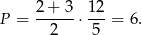
Odpowiedź: 6

