/Konkursy/Zadania testowe/Kombinatoryka/Figury magiczne

Zadanie nr 2128911

Dodaj do ulubionych
Dodaj do rozwiązanych

Z siatki składającej się z 8 trójkątów równobocznych można skleić ośmiościan foremny, jak na rysunku obok. Aby powstał ośmiościan magiczny, trzeba zamienić litery 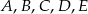A ,B,C ,D ,E na liczby 2,4,6,7,8 (każdą literę na inną liczbę) w ten sposób, by sumy liczb na czterech ścianach przy każdym wierzchołku były sobie równe. Ile wówczas będzie równe B + D ?

PIC

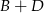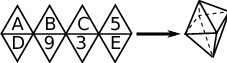
A) 6 B) 7 C) 8 D) 9 E) 10

Rozwiązanie

Ponieważ suma wszystkich liczb to

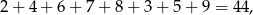
2+ 4+ 6 + 7 + 8 + 3 + 5 + 9 = 4 4,

więc suma przy każdym wierzchołku ma wynosić 22. Patrząc na wierzchołek wspólny ścian 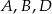A ,B ,D i 9, mamy

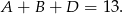
A + B + D = 13.

Ale wśród podanych liczb jest tylko jedna liczba nieparzysta, zatem wśród tych liczb musi być 7, a dwie pozostałe to 2 i 4 (bo suma ma być 6). Pozostało ustalić, gdzie jest 7.

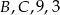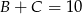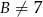Patrzymy teraz wierzchołek wspólny B,C ,9,3 . Mamy B + C = 1 0 zatem B ⁄= 7 . Podobnie, jak popatrzymy na wierzchołek wspólny ścian 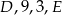D ,9,3,E , to otrzymamy 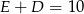E + D = 10 , czyli D ⁄= 7 .

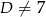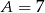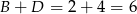Zatem A = 7 i B + D = 2 + 4 = 6 .  
Odpowiedź: A

Wersja PDF