Zadanie nr 6740664
W polach szachownicy 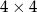 chcemy umieścić pionki w taki sposób, że liczby pionków w każdym wierszu i w każdej kolumnie szachownicy będą różne (w jednym polu można umieścić jeden lub więcej pionków, a także można pozostawić pole puste). Jaka jest minimalna liczba pionków, które można w taki sposób rozmieścić na szachownicy?
chcemy umieścić pionki w taki sposób, że liczby pionków w każdym wierszu i w każdej kolumnie szachownicy będą różne (w jednym polu można umieścić jeden lub więcej pionków, a także można pozostawić pole puste). Jaka jest minimalna liczba pionków, które można w taki sposób rozmieścić na szachownicy?
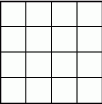
A) 7 B) 10 C) 14 D) 18 E) 28
Rozwiązanie
Kwadrat ma w sumie 8 wierszy i kolumn, więc minimalna suma różnych sum otrzymanych w opisany sposób to
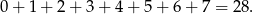
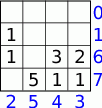
To jest prawie minimalna liczba pionków – jedyny problem to, że każdego pionka policzyliśmy dwa razy (raz w wierszu i raz w kolumnie). Zatem najmniejsza możliwa liczba pionków to 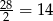 . Pozostało sprawdzić, że rzeczywiście da się znaleźć dobrą konfigurację z 14 pionkami. Konfiguracji takiej szukamy metodą prób i błędów.
. Pozostało sprawdzić, że rzeczywiście da się znaleźć dobrą konfigurację z 14 pionkami. Konfiguracji takiej szukamy metodą prób i błędów.
Odpowiedź: C

