Zadanie nr 1065621
Na bokach 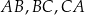 trójkąta równobocznego
trójkąta równobocznego 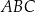 wybrano kolejno punkty
wybrano kolejno punkty 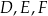 tak, że
tak, że 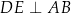 ,
, 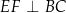 i
i 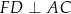 .
.

Wykaż, że trójkąt 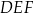 jest trójkątem równobocznym o polu trzy razy mniejszym od pola trójkąta
jest trójkątem równobocznym o polu trzy razy mniejszym od pola trójkąta 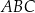 .
.
Rozwiązanie
Zauważmy, że każdy z trójkątów 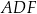 ,
, 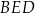 i
i 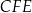 jest trójkątem prostokątnym z kątem
jest trójkątem prostokątnym z kątem 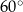 , czyli połówką trójkąta równobocznego. Jeżeli więc oznaczymy
, czyli połówką trójkąta równobocznego. Jeżeli więc oznaczymy 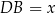 ,
, 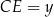 i
i 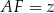 , to
, to 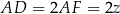 ,
, 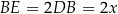 i
i 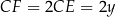 .
.

Stąd
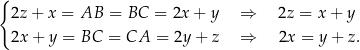
Jeżeli odejmiemy od pierwszego z tych równań drugie, to mamy

Stąd 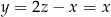 i wszystkie trzy trójkąty
i wszystkie trzy trójkąty 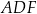 ,
, 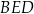 i
i 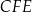 są przystające. To oczywiście oznacza, że trójkąt
są przystające. To oczywiście oznacza, że trójkąt 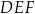 jest równoboczny. Musimy jeszcze wyznaczyć skalę podobieństwa
jest równoboczny. Musimy jeszcze wyznaczyć skalę podobieństwa 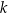 tego trójkąta z trójkątem
tego trójkąta z trójkątem 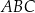 . Zauważmy, że
. Zauważmy, że
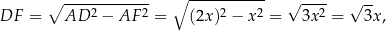
więc
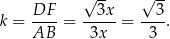
Ponieważ pole zmienia się jak kwadrat skali podobieństwa, mamy stąd