/Szkoła średnia/Geometria/Planimetria/Trójkąt/Równoboczny

Zadanie nr 1281792

Dodaj do ulubionych
Dodaj do rozwiązanych

W trójkącie równobocznym 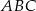ABC połączono środki wysokości otrzymując trójkąt 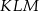KLM . Oblicz stosunek pól trójkątów 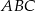ABC i KLM .

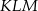Rozwiązanie

Rozpoczynamy oczywiście od rysunku.

PIC

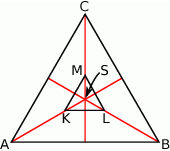
Wiemy, że środek trójkąta równobocznego dzieli wysokości w stosunku 2:1, więc jeżeli oznaczymy przez 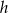h długość wysokości trójkąta 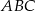ABC to

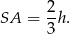
2- SA = 3h.

Wiemy też, że 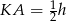KA = 12 h . Zatem

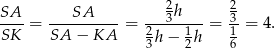
SA-- ---SA----- ---23h--- 23- SK = SA − KA = 2 1 = 1 = 4. 3h − 2h 6

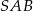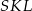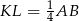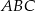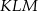To oznacza, że trójkąty SAB i SKL są podobne w skali 4:1, czyli 1 KL = 4 AB . To z kolei oznacza, że trójkąty ABC i KLM są podobne w skali 4:1, czyli stosunek ich pól jest równy 16.  
Odpowiedź: 16

Wersja PDF