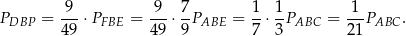Zadanie nr 2087676
Dany jest trójkąt równoboczny 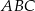 . Na bokach
. Na bokach 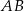 i
i 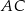 wybrano punkty – odpowiednio –
wybrano punkty – odpowiednio – 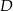 i
i 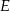 takie, że
takie, że 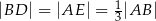 . Odcinki
. Odcinki 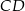 i
i 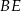 przecinają się w punkcie
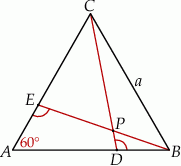
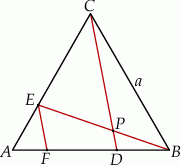
przecinają się w punkcie 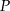 (zobacz rysunek).
(zobacz rysunek).
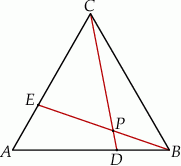
Wykaż, że pole trójkąta 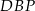 jest 21 razy mniejsze od pola trójkąta
jest 21 razy mniejsze od pola trójkąta 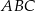 .
.
Rozwiązanie
Niech  będzie długością boku trójkąta
będzie długością boku trójkąta 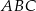 .
.
Sposób I
Zauważmy, że trójkąty 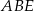 i
i 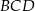 mają dwa takie same boki i kąt o mierze
mają dwa takie same boki i kąt o mierze 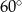 między tymi bokami.
między tymi bokami.
Są więc przystające i
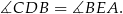
To zaś oznacza, że trójkąty 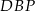 i
i 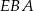 mają dwa takie same kąty, czyli są podobne. Aby wyznaczyć ich skalę podobieństwa, obliczymy długość odcinka
mają dwa takie same kąty, czyli są podobne. Aby wyznaczyć ich skalę podobieństwa, obliczymy długość odcinka 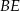 . Stosujemy twierdzenie cosinusów w trójkącie
. Stosujemy twierdzenie cosinusów w trójkącie 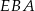 .
.
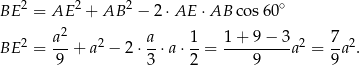
To oznacza, że
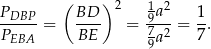
Zauważmy jeszcze, że trójkąty 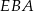 i
i 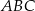 mają wspólną wysokość opuszczoną z wierzchołka
mają wspólną wysokość opuszczoną z wierzchołka 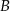 , więc
, więc
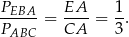
Mamy zatem
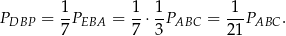
Sposób II
Niech 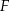 będzie takim punktem odcinka
będzie takim punktem odcinka 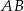 , że
, że 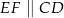 .
.
Wiemy że
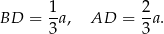
Trójkąty 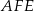 i
i 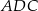 są podobne, więc
są podobne, więc
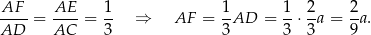
Stąd
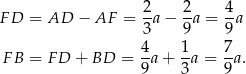
Patrzymy teraz na trójkąty podobne 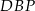 i
i 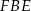 . Ich skala podobieństwa
. Ich skala podobieństwa 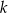 to
to
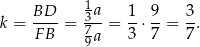
Zatem
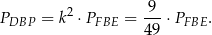
Trójkąty 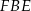 i
i 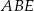 mają wspólną wysokość opuszczoną z wierzchołka
mają wspólną wysokość opuszczoną z wierzchołka 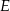 , więc
, więc
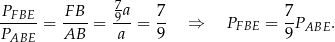
Podobna sytuacja ma też miejsce w przypadku trójkątów 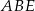 i
i 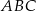 – mają wspólną wysokość opuszczoną z wierzchołka
– mają wspólną wysokość opuszczoną z wierzchołka 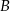 . Zatem
. Zatem
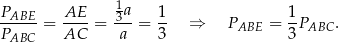
Łączymy wszystkie otrzymane równości i mamy