Zadanie nr 3315086
W trójkąt równoboczny 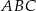 wpisano trójkąt
wpisano trójkąt 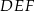 (patrz rysunek), tak że
(patrz rysunek), tak że 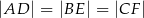 . Udowodnij, że trójkąt
. Udowodnij, że trójkąt 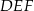 jest równoboczny.
jest równoboczny.
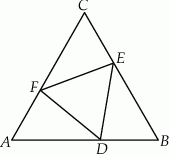
Rozwiązanie
Sposób I
Zauważmy, że trójkąty 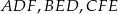 mają kąt mierze
mają kąt mierze 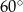 oraz odcinki przylegające do tego kąta w każdym z trójkątów mają tę samą długość. To oznacza, że trójkąty te są przystające. Zatem
oraz odcinki przylegające do tego kąta w każdym z trójkątów mają tę samą długość. To oznacza, że trójkąty te są przystające. Zatem
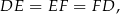
czyli trójkąt 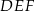 jest równoboczny.
jest równoboczny.
Sposób II
Niech 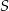 będzie środkiem trójkąta
będzie środkiem trójkąta 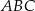 , a
, a 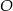 obrotem płaszczyzny o kąt
obrotem płaszczyzny o kąt 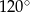 wokół punktu
wokół punktu 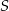 .
.
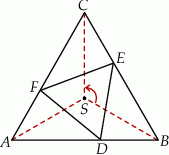
Zauważmy, że obrót 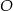 przekształca odcinek
przekształca odcinek 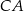 na odcinek
na odcinek 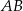 . Ponadto punkt
. Ponadto punkt 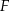 zostanie przekształcony na punkt odcinka
zostanie przekształcony na punkt odcinka 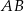 , który jest w odległości
, który jest w odległości 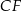 od punktu
od punktu 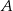 , czyli na punkt
, czyli na punkt 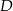 . Analogicznie uzasadniamy, że
. Analogicznie uzasadniamy, że 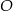 przekształca
przekształca 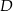 na
na 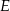 i
i 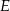 na
na 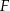 . To jednak oznacza, że trójkąt
. To jednak oznacza, że trójkąt 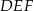 przechodzi na siebie przy obrocie o
przechodzi na siebie przy obrocie o 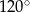 , musi to więc być trójkąt równoboczny (bo np. wszystkie jego boki muszą mieć tę samą długość).
, musi to więc być trójkąt równoboczny (bo np. wszystkie jego boki muszą mieć tę samą długość).

