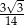Zadanie nr 4458470
Dany jest trójkąt równoboczny 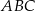 o boku długości 16. Na boku
o boku długości 16. Na boku 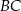 obrano punkt
obrano punkt 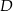 dzielący ten bok w stosunku 3:5, licząc od punktu
dzielący ten bok w stosunku 3:5, licząc od punktu 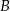 . Oblicz sinus kąta
. Oblicz sinus kąta 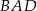 .
.
Rozwiązanie
Zacznijmy od rysunku.
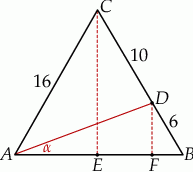
Zauważmy, że z podanych informacji mamy
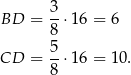
Sposob I
Obliczmy najpierw długość odcinka  (z twierdzenia cosinusów).
(z twierdzenia cosinusów).
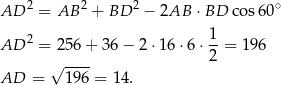
Stosujemy teraz twierdzenie sinusów w trójkącie 

Sposób II
Zauważmy, że 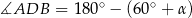 , więc stosując wzór na sinus sumy mamy
, więc stosując wzór na sinus sumy mamy
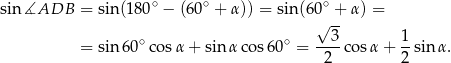
Stosujemy teraz twierdzenie sinusów w trójkącie 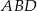 .
.
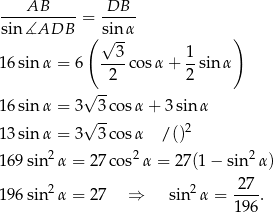
Ponieważ  jest kątem ostrym, mamy stąd
jest kątem ostrym, mamy stąd
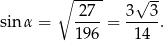
Sposob III
Zadanie ma znacznie prostsze rozwiązanie, jeżeli wykorzystamy odrobinę więcej geometrii. Dorysujmy wysokość 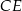 oraz równoległy do niej odcinek
oraz równoległy do niej odcinek 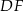 . Szukany sinus możemy obliczyć z trójkąta prostokątnego
. Szukany sinus możemy obliczyć z trójkąta prostokątnego 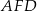 , aby jednak móc to zrobić musimy najpierw obliczyć długości odcinków
, aby jednak móc to zrobić musimy najpierw obliczyć długości odcinków 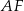 i
i 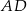 . Trójkąty
. Trójkąty 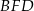 i
i 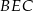 są podobne oraz znamy ich skalę podobieństwa
są podobne oraz znamy ich skalę podobieństwa
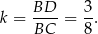
Mamy stąd
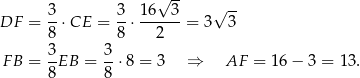
Mamy zatem
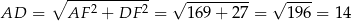
oraz
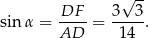
Odpowiedź: