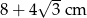/Szkoła średnia/Geometria/Planimetria/Trójkąt/Równoboczny

Zadanie nr 5425749

Dodaj do ulubionych
Dodaj do rozwiązanych

Oblicz długość boku trójkąta równobocznego, wiedząc, że bok ten jest o 2 cm dłuższy od wysokości tego trójkąta.

Rozwiązanie

Zaczynamy od rysunku

PIC

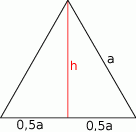
Z założenia mamy 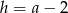h = a− 2 .

Sposób I

Z zależności między wysokością, a bokiem trójkąta równobocznego otrzymujemy

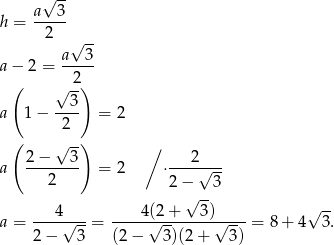
a√ 3- h = ----- 2 √ -- a 3 a − 2 = -2--- ( √ -) --3- a 1 − 2 = 2 ( √ -) ∕ 2− 3 2 a -------- = 2 ⋅----√--- 2 2 − 3 4 4 (2 + √ 3-) √ -- a = ----√---= -----√--------√----= 8 + 4 3. 2− 3 (2 − 3)(2 + 3 )

Sposób II

Na mocy twierdzenia Pitagorasa mamy

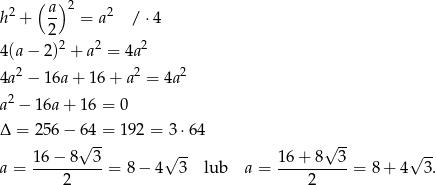
( a) 2 h2 + -- = a2 / ⋅4 2 4(a − 2)2 + a2 = 4a 2 2 2 2 4a − 16a + 16 + a = 4a a2 − 16a + 16 = 0 Δ = 256 − 6√4-= 192 = 3 ⋅64 √ -- 16− 8 3 √ -- 16 + 8 3 √ -- a = ----------= 8 − 4 3 lub a = ----------= 8 + 4 3. 2 2

Pierwsza liczba jest ujemna, więc 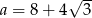√ -- a = 8 + 4 3 .  
Odpowiedź: √ -- 8 + 4 3 cm

Wersja PDF