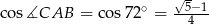Zadanie nr 3024938
W trójkącie równoramiennym 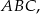 w którym
w którym 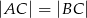 i
i 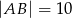 , poprowadzono dwusieczną kąta
, poprowadzono dwusieczną kąta 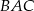 przecinająca bok
przecinająca bok 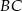 w punkcie
w punkcie 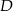 . Wówczas okazało się, że
. Wówczas okazało się, że 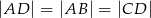 .
.
- Wyznacz miary kątów trójkąta
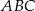 .
. - Oblicz długość ramienia
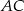 .
. - Oblicz
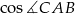 .
.
Rozwiązanie
Zaczynamy od rysunku.
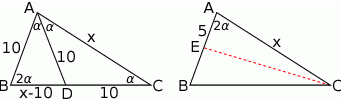
- Jeżeli oznaczymy kąt przy podstawie trójkąta
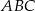 przez
przez 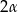 , to ponieważ trójkąt
, to ponieważ trójkąt 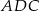 jest równoramienny, to
jest równoramienny, to 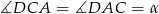 . Zatem (z sumy kątów w trójkącie
. Zatem (z sumy kątów w trójkącie 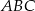 )
) 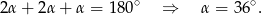
Odpowiedź: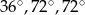
- Jeżeli oznaczymy szukaną długość przez
 to z podobieństwa trójkątów
to z podobieństwa trójkątów 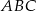 i
i 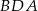 mamy
mamy 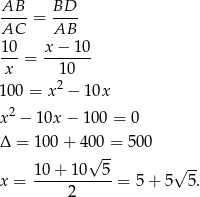
Odpowiedź: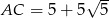
- Jeżeli poprowadzimy wysokość
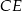 to z trójkąta prostokątnego
to z trójkąta prostokątnego 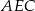 mamy
mamy 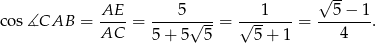
Odpowiedź: