/Szkoła średnia/Geometria/Planimetria/Trójkąt/Równoramienny

Zadanie nr 3054663

Dodaj do ulubionych
Dodaj do rozwiązanych

W trójkącie równoramiennym podstawa ma długość 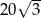√ -- 20 3 . Pole trójkąta jest równe 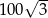√ -- 10 0 3 . Oblicz obwód tego trójkąta i miarę kąta przy podstawie.

Rozwiązanie

Zaczynamy od rysunku.

PIC

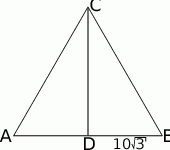
Korzystając z podanego pola, wyliczmy wysokość 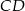CD .

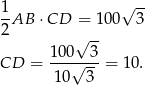
√ -- 1-AB ⋅ CD = 10 0 3 2 √ -- 100 3 CD = ---√---= 10. 10 3

Teraz z twierdzenia Pitagorasa liczymy ramię trójkąta.

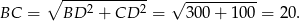
∘ ---2-------2 √ ---------- BC = BD + CD = 300 + 100 = 20.

Zatem obwód jest równy

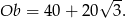
√ -- Ob = 4 0+ 20 3.

Mamy ponadto

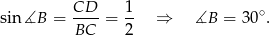
CD 1 sin ∡B = ---- = -- ⇒ ∡B = 30∘. BC 2

 
Odpowiedź: Obwód: 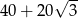√ -- 40 + 20 3 , kąt: ∘ 30

Wersja PDF