/Szkoła średnia/Geometria/Planimetria/Trójkąt/Równoramienny

Zadanie nr 3319261

Dodaj do ulubionych
Dodaj do rozwiązanych

W trójkącie równoramiennym wysokość opuszczona na podstawę jest równa 36, a promień okręgu wpisanego w ten trójkąt jest równy 10. Oblicz długości boków tego trójkąta i promień okręgu opisanego na tym trójkącie.

Rozwiązanie

Zacznijmy od rysunku i oznaczmy długość podstawy trójkąta przez 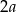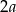2a (2a , a nie a , żeby nie mieć ułamków).

PIC

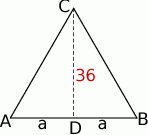
Aby wykorzystać podaną informację o promieniu okręgu wpisanego w trójkąt 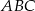ABC , będziemy chcieli skorzystać ze wzoru na pole 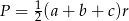P = 12(a + b + c)r . Aby to zrobić obliczamy długość ramienia trójkąta.

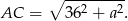
∘ --------- AC = 362 + a2.

Zapiszmy teraz podaną informację o długości promienia wpisanego w trójkąt.

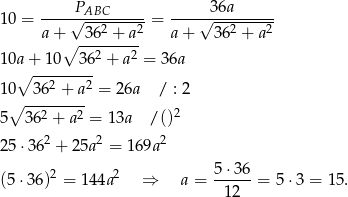
PABC 36a 10 = ----√---2----2-= ---√----2----2- a+ ∘ -36-+--a- a+ 3 6 + a 10a + 10 362 + a2 = 36a ∘ --------- 10 362 + a2 = 26a / : 2 ∘ --------- 2 5 362 + a2 = 13a /() 25 ⋅362 + 25a2 = 169a2 (5 ⋅36)2 = 14 4a2 ⇒ a = 5-⋅36-= 5⋅ 3 = 15. 12

Ramię trójkąta jest więc równe

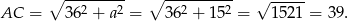
∘ --------- ∘ ---------- √ ----- AC = 362 + a2 = 362 + 152 = 152 1 = 39.

Promień okręgu opisanego na trójkącie 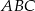ABC obliczymy na trzy sposoby.

Sposób I

Korzystamy ze wzoru 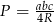abc- P = 4R na pole trójkąta. Mamy więc

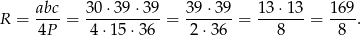
abc 30 ⋅39 ⋅39 39 ⋅39 13⋅ 13 1 69 R = ----= -----------= -------= -------= ----. 4P 4⋅1 5⋅36 2 ⋅36 8 8

Sposób II

Korzystając ze wzoru na pole z sinusem mamy

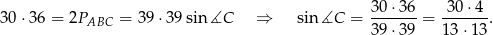
30-⋅36- 30-⋅4-- 30 ⋅36 = 2PABC = 39 ⋅39 sin ∡C ⇒ sin ∡C = 39 ⋅39 = 13⋅ 13.

Korzystamy teraz z twierdzenia sinusów

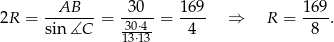
AB 30 169 169 2R = ------- = 30⋅4-= ---- ⇒ R = ---. sin ∡C 13⋅13 4 8

Sposób III

W trójkącie prostokątnym 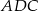ADC mamy

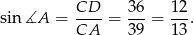
CD 36 12 sin ∡A = CA--= 39-= 13-.

Korzystamy teraz z twierdzenia sinusów

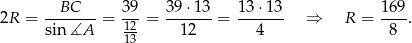
--BC--- 39- 3-9⋅13- 13-⋅13- 169- 2R = sin∡A = 12 = 1 2 = 4 ⇒ R = 8 . 13

 
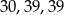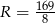Odpowiedź: Długości boków: 30,39,3 9 , promień okręgu opisanego: R = 1689- .

Wersja PDF