/Szkoła średnia/Geometria/Planimetria/Trójkąt/Równoramienny

Zadanie nr 3986470

Dodaj do ulubionych
Dodaj do rozwiązanych

W trójkącie równoramiennym 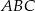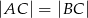ABC (|AC | = |BC | ) dwusieczna 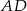AD ma długość 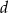d a miara kąta 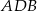ADB wynosi α . Oblicz długość promienia okręgu wpisanego w ten trójkąt.

Rozwiązanie

Zaczynamy od rysunku.

PIC

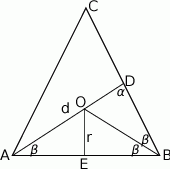
Poprowadźmy drugą dwusieczną, przetnie ona 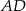AD w środku 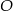O okręgu wpisanego w trójkąt 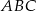ABC . Musimy wyliczyć odległość 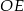OE punktu 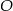O od boku 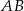AB . Jeżeli oznaczymy

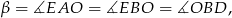
β = ∡EAO = ∡EBO = ∡OBD ,

to licząc sumę kątów trójkąta 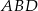ABD mamy

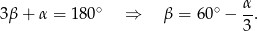
∘ ∘ α- 3β + α = 180 ⇒ β = 60 − 3.

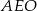Będziemy zmierzać do wyliczenia r z trójkąta prostokątnego AEO . Najpierw jednak wyliczmy 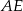AE . Z twierdzenia sinusów w trójkącie 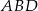ABD mamy

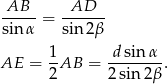
AB AD sin-α-= sin2β- AE = 1-AB = -dsin-α-. 2 2 sin 2β

Zatem

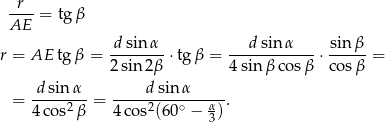
-r-- AE = tg β d sin α dsin α sin β r = AE tg β = --------⋅tgβ = ------------⋅ -----= 2sin2 β 4sin β cosβ cosβ dsin α dsinα = -----2--= -----2---∘---α-. 4c os β 4 cos (60 − 3)

 
Odpowiedź: 4-cosd2si(6n0α∘−-α) 3

Wersja PDF