Zadanie nr 5481172
Odcinki 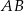 oraz
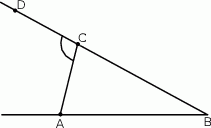
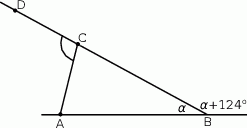
oraz 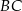 (rysunek) są równej długości. Kąt
(rysunek) są równej długości. Kąt 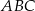 ma miarę o
ma miarę o 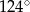 mniejszą od miary kąta do niego przyległego. Oblicz miarę kąta
mniejszą od miary kąta do niego przyległego. Oblicz miarę kąta 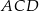 .
.
Rozwiązanie
Oznaczmy 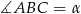 .
.
Wiemy wtedy, że kąt przyległy do kąta 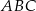 ma miarę
ma miarę 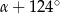 , więc
, więc

Trójkąt 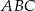 jest równoramienny, więc
jest równoramienny, więc
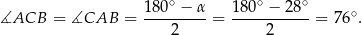
Stąd
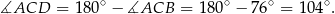
Odpowiedź: