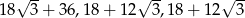/Szkoła średnia/Geometria/Planimetria/Trójkąt/Równoramienny

Zadanie nr 5643459

Dodaj do ulubionych
Dodaj do rozwiązanych

Na okręgu o promieniu 9 opisano trójkąt równoramienny o kącie równym 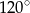12 0∘ . Oblicz długości boków trójkąta.

Rozwiązanie

Kąt rozwarty 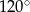∘ 120 musi być kątem między ramionami trójkąta – kąty przy podstawie nie mogą mieć miary 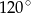12 0∘ , bo trójkąt nie może mieć dwóch kątów rozwartych.

PIC

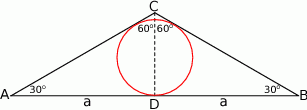
Sposób I

Niech 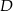D będzie środkiem podstawy 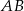AB trójkąta, oraz niech 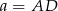a = AD . Z trójkąta prostokątnego 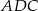ADC mamy

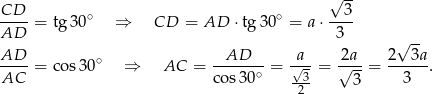
√ -- CD-- ∘ ∘ --3- AD = tg 30 ⇒ CD = AD ⋅ tg 30 = a ⋅ 3 AD AD a 2a 2 √ 3a ----= cos30 ∘ ⇒ AC = -------= √-- = √---= ------. AC cos30∘ --3 3 3 2

Korzystamy teraz ze wzoru na pole trójkąta z promieniem okręgu wpisanego.

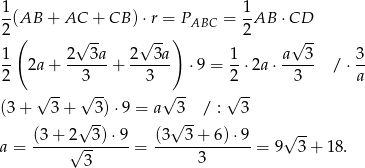
1 1 --(AB + AC + CB )⋅ r = PABC = --AB ⋅CD 2 ( √ -- √ --) 2 √ -- 1 2 3a 2 3a 1 a 3 3 -- 2a + ------+ ------ ⋅9 = --⋅2a ⋅ ----- / ⋅ -- 2 3 3 2 3 a (3 + √ 3-+ √ 3)⋅ 9 = a√ 3- / : √ 3 √ -- √ -- (3 + 2 3)⋅9 (3 3 + 6) ⋅9 √ -- a = -----√------- = ------3------ = 9 3+ 18. 3

Zatem boki trójkąta mają długości:

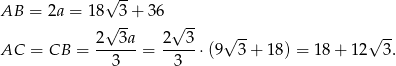
√ -- AB = 2a = 18√ 3-+ 36 √ -- 2 3a 2 3 √ -- √ -- AC = CB = ------= -----⋅(9 3 + 1 8) = 18 + 12 3. 3 3

Sposób II

Oznaczmy przez 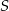S środek okręgu wpisanego, a przez 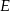E jego punkt styczności z bokiem AC .

PIC

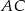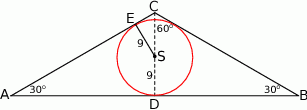
Z trójkąta prostokątnego 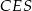CES mamy

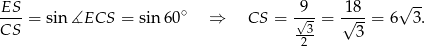
ES- ∘ -9- 18-- √ -- CS = sin ∡ECS = sin6 0 ⇒ CS = √-3 = √ 3 = 6 3 . 2

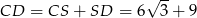Stąd √ -- CD = CS + SD = 6 3+ 9 . Teraz patrzymy na trójkąt prostokątny ADC .

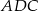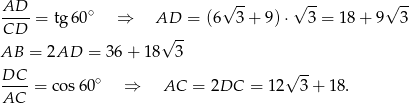
AD √ -- √ -- √ -- ---- = tg 60∘ ⇒ AD = (6 3 + 9) ⋅ 3 = 1 8+ 9 3 CD √ -- AB = 2AD = 36+ 18 3 DC √ -- ---- = cos 60∘ ⇒ AC = 2DC = 12 3 + 18. AC

 
Odpowiedź: √ -- √ -- √ -- 18 3 + 3 6,18+ 12 3,18 + 12 3

Wersja PDF