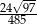Zadanie nr 5747474
Dany jest trójkąt równoramienny 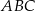 , w którym podstawa
, w którym podstawa 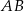 ma długość 12, a każde z ramion
ma długość 12, a każde z ramion 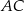 i
i 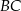 ma długość równą 10. Punkt
ma długość równą 10. Punkt 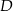 jest środkiem ramienia
jest środkiem ramienia 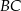 (zobacz rysunek).
(zobacz rysunek).
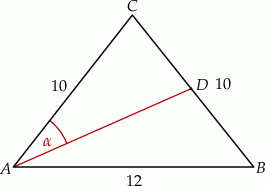
Oblicz sinus kąta  , jaki środkowa
, jaki środkowa 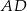 tworzy z ramieniem
tworzy z ramieniem 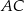 trójkąta
trójkąta 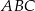 .
.
Rozwiązanie
Dorysujmy wysokość 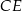 i rzut
i rzut 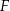 punktu
punktu 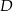 na podstawę
na podstawę 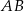 .
.
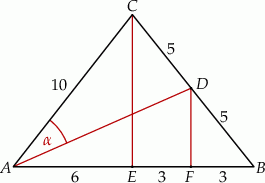
Korzystamy z twierdzenia Pitagorasa w trójkącie 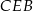 i obliczamy długość wysokości
i obliczamy długość wysokości 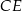

Prosta 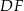 jest równoległa do
jest równoległa do 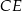 i przechodzi przez środek
i przechodzi przez środek 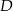 odcinka
odcinka 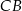 , więc
, więc 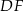 jest odcinkiem łączącym środki boków w trójkącie
jest odcinkiem łączącym środki boków w trójkącie 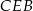 . W szczególności
. W szczególności
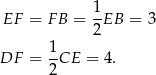
Ponownie korzystamy z twierdzenia Pitagorasa – tym razem w trójkącie 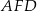 .
.
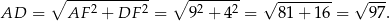
Zauważmy teraz, że trójkąty 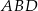 i
i 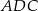 mają podstawy równej długości
mają podstawy równej długości 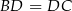 oraz wspólną wysokość opuszczoną z wierzchołka
oraz wspólną wysokość opuszczoną z wierzchołka 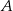 na te podstawy. To oznacza, że mają równe pola. Stąd
na te podstawy. To oznacza, że mają równe pola. Stąd
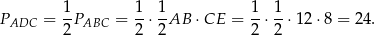
Teraz możemy już obliczyć interesujący nas sinus – korzystamy ze wzoru na pole trójkąta z sinusem.
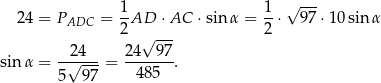
Odpowiedź: