Zadanie nr 5844773
Punkt 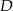 leży na boku
leży na boku 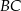 trójkąta równoramiennego
trójkąta równoramiennego 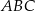 , w którym
, w którym 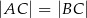 .
.
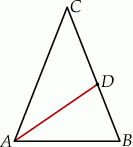
Odcinek 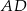 dzieli trójkąt
dzieli trójkąt 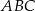 na dwa trójkąty równoramienne w taki sposób, że
na dwa trójkąty równoramienne w taki sposób, że 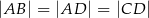 . Oblicz miary kątów trójkąta
. Oblicz miary kątów trójkąta 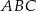 .
.
Rozwiązanie
Oznaczmy 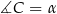 .
.
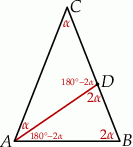
Ponieważ trójkąt 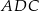 jest równoramienny, mamy
jest równoramienny, mamy
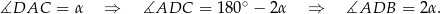
Wiemy również, że trójkąt 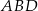 jest równoramienny, czyli
jest równoramienny, czyli
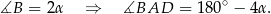
Teraz pozostało skorzystać z tego, że wyjściowy trójkąt jest równoramienny.
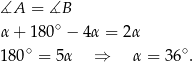
Zatem kąty trójkąta 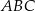 są równe
są równe 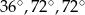 .
.
Odpowiedź: