Zadanie nr 6684612
W trójkąt równoramienny wpisano kwadrat w ten sposób, że dwa jego wierzchołki leżą na podstawie trójkąta, a dwa pozostałe są środkami ramion. Jaką część pola trójkąta stanowi pole kwadratu? Odpowiedź uzasadnij.
Rozwiązanie
Zaczynamy oczywiście od rysunku.
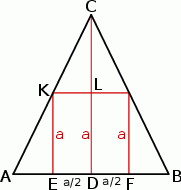
Zauważmy, że trójkąty prostokątne 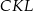 i
i 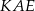 są podobne (bo mają równe kąty) oraz
są podobne (bo mają równe kąty) oraz 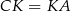 (bo z założenia
(bo z założenia 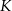 jest środkiem
jest środkiem 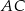 ). W takim razie trójkąty te są przystające i
). W takim razie trójkąty te są przystające i
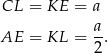
W takim razie
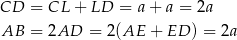
i pole trójkąta 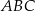 jest równe
jest równe
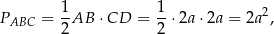
czyli jest dwa razy większe od pola kwadratu.
Odpowiedź: