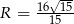/Szkoła średnia/Geometria/Planimetria/Trójkąt/Równoramienny

Zadanie nr 6865108

Dodaj do ulubionych
Dodaj do rozwiązanych

Podstawa 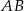AB trójkąta równoramiennego 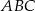ABC ma długość 4, a ramiona mają długość 8.

  • Oblicz długość promienia okręgu wpisanego w ten trójkąt.
  • Oblicz dlugość promienia okręgu opisanego na tym trójkącie.

Rozwiązanie

Zaczynamy od rysunku.

PIC

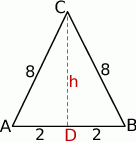
  • Promień okręgu wpisanego obliczymy ze wzoru na pole
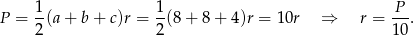
    P = 1(a + b + c)r = 1(8 + 8+ 4)r = 10r ⇒ r = P-. 2 2 10

    Aby dokończyć ten rachunek, musimy obliczyć pole trójkąta 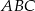ABC . Najpierw liczymy długość jego wysokości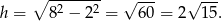

    ∘ ------- √ --- √ --- h = 82 − 22 = 60 = 2 15.

    Zatem pole jest równe

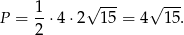
    1 √ --- √ --- P = --⋅4⋅ 2 15 = 4 1 5. 2

    Stąd promień

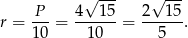
    √ --- √ --- P 4 15 2 15 r = ---= ------= ------. 10 10 5

     
    Odpowiedź: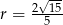 √-- r = 2-155-

  •  

    Sposób I

    Skorzystamy ze wzoru na pole trójkąta

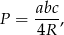
    abc P = ---, 4R

    gdzie 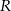R – promień okręgu opisanego na trójkącie. Mamy więc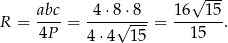

    √ --- abc- -4⋅8-⋅8-- 16--15- R = 4P = √ ---= 15 . 4⋅ 4 15

    Sposób II

    Jeżeli nie znamy lub nie pamiętamy wzoru z poprzedniego sposobu, to możemy skorzystać z twierdzenia sinusów.

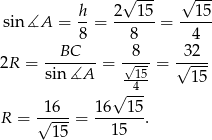
    √ --- √ --- h- 2---15 --15- sin ∡A = 8 = 8 = 4 BC 8 32 2R = ------- = √---= √---- sin∡A -145- 15 √ --- R = √16--= 16--15-. 15 15

     
    Odpowiedź: 16√ 15 R = -15--

Wersja PDF