Zadanie nr 7588109
Dany jest trójkąt równoramienny 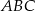 , w którym
, w którym 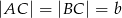 i
i 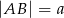 . Punkty
. Punkty 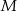 i
i 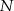 są rzutami prostopadłymi środka podstawy
są rzutami prostopadłymi środka podstawy 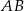 trójkąta na ramiona
trójkąta na ramiona 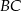 i
i 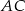 . Wyraź pole czworokąta
. Wyraź pole czworokąta 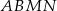 za pomocą
za pomocą  i
i 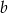 .
.
Rozwiązanie
Zaczynamy od rysunku.
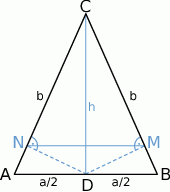
Pole trapezu 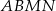 możemy obliczyć jako różnicę pól trójkątów
możemy obliczyć jako różnicę pól trójkątów 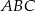 i
i 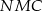 . Co więcej, trójkąt
. Co więcej, trójkąt 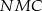 jest podobny do trójkąta
jest podobny do trójkąta 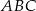 i dość łatwo jest obliczyć skalę
i dość łatwo jest obliczyć skalę 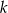 tego podobieństwa. Z podobieństwa trójkątów prostokątnych
tego podobieństwa. Z podobieństwa trójkątów prostokątnych 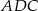 i
i 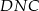 mamy
mamy
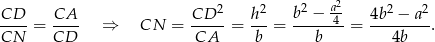
W takim razie
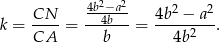
Pole zmienia się jak kwadrat skali podobieństwa, więc
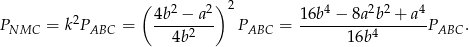
Pozostało obliczyć pole trapezu 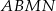 .
.
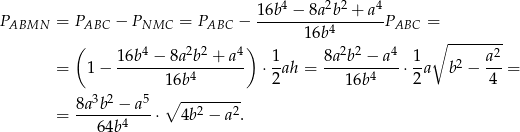
Odpowiedź: