Zadanie nr 7590763
Dany jest trójkąt równoramienny 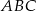 , w którym
, w którym 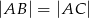 i
i 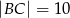 . Na boku
. Na boku 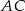 wybrano punkt
wybrano punkt 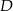 w ten sposób, że
w ten sposób, że 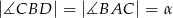 oraz
oraz 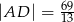 . Oblicz
. Oblicz 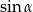 .
.
Rozwiązanie
Rozpoczynamy oczywiście od rysunku.
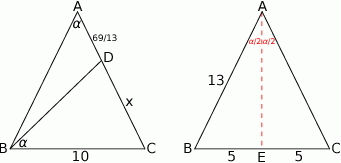
Zauważmy, że trójkąty 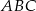 i
i 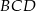 mają dwa takie same kąty:
mają dwa takie same kąty:  i
i 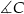 . W takim razie są podobne i jeżeli oznaczymy
. W takim razie są podobne i jeżeli oznaczymy 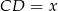 to mamy
to mamy
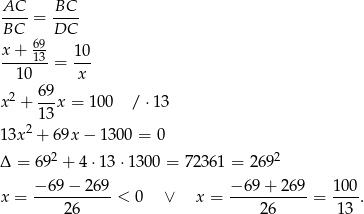
Zatem
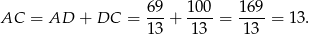
Wartość 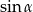 obliczymy na dwa sposoby.
obliczymy na dwa sposoby.
Sposób I
Aby obliczyć 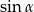 dorysujmy wysokość
dorysujmy wysokość 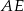 trójkąta
trójkąta 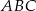 . W trójkącie prostokątnym
. W trójkącie prostokątnym 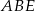 mamy
mamy
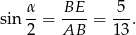
Zatem
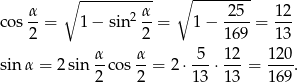
Sposób II
Tym razem piszemy twierdzenie cosinusów w trójkącie 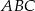 .
.
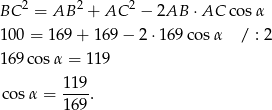
Teraz obliczamy 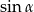 (korzystamy z tego, że
(korzystamy z tego, że 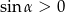 dla
dla 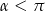 ).
).
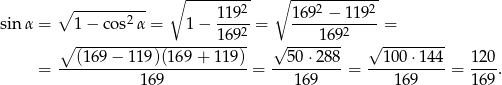
Odpowiedź: