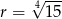/Szkoła średnia/Geometria/Planimetria/Trójkąt/Równoramienny

Zadanie nr 7860282

Dodaj do ulubionych
Dodaj do rozwiązanych

Pole trójkąta równoramiennego jest równe 25. Oblicz długość promienia okręgu wpisanego w trójkąt wiedząc, że ramię jest dwa razy dłuższe od podstawy.

Rozwiązanie

Zacznijmy od rysunku i oznaczmy długość podstawy przez 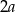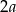2a (2a , a nie a , żeby nie mieć ułamków).

PIC

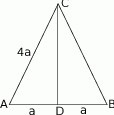
Wiemy wtedy, że ramię ma długość 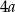4a . Z trójkąta prostokątnego 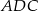ADC (gdzie 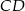CD – wysokość opuszczona z wierzchołka 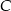C ) wyliczamy wysokość trójkąta

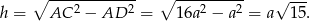
∘ ------------ ∘ ---------- √ --- h = AC 2 − AD 2 = 16a2 − a2 = a 15 .

Z podanego pola mamy

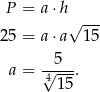
P = a⋅h √ --- 25 = a⋅a 1 5 5 a = 4√---. 15

Aby wyliczyć promień okręgu wpisanego w trójkąt skorzystamy ze wzoru na pole

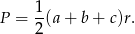
1 P = -(a+ b+ c)r. 2

W naszej sytuacji

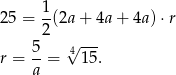
1 25 = -(2a + 4a + 4a) ⋅r 2 √ --- r = 5-= 415. a

 
Odpowiedź: √4--- r = 15

Wersja PDF