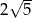/Szkoła średnia/Geometria/Planimetria/Trójkąt/Równoramienny

Zadanie nr 7927410

Dodaj do ulubionych
Dodaj do rozwiązanych

Podstawa trójkąta równoramiennego ma długość 4. Środek okręgu opisanego na tym trójkącie dzieli jedną z wysokości trójkąta na odcinki, których stosunek długości wynosi 3:5. Oblicz długość ramienia trójkąta.

Rozwiązanie

Naszkicujmy opisaną sytuację.

PIC

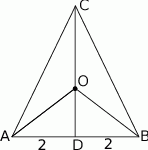
Najważniejszą rzeczą jest ustalenie, o której wysokości jest mowa w treści zadania. Gdyby środek 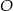O okręgu opisanego leżał na wysokości opuszczonej z wierzchołka 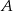A , to oznaczałoby to, że symetralna boku 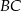BC przechodzi przez wierzchołek 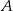A , czyli trójkąt byłby równoboczny. Wtedy jednak środek okręgu opisanego dzieli wysokości w stosunku 2:1. Podobnie uzasadniamy, że opisana sytuacja nie może dotyczyć wysokości opuszczonej z wierzchołka B .

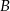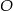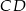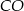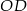Wiemy zatem, że punkt O dzieli wysokość CD w stosunku 3:5. Pozostało ustalić, który z odcinków CO , czy OD jest dłuższy. To jednak jest jasne z trójkąta prostokątnego 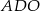ADO . Ponieważ 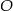O jest środkiem okręgu opisanego, mamy

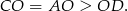
CO = AO > OD .

Zatem wiemy, że

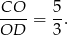
-CO- = 5. OD 3

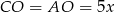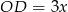Jeżeli oznaczymy CO = AO = 5x i OD = 3x , to z trójkąta prostokątnego 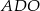ADO mamy

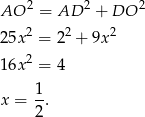
2 2 2 AO = AD + DO 25x 2 = 22 + 9x2 16x 2 = 4 1 x = -. 2

Możemy teraz wyliczyć wysokość trójkąta

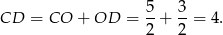
5 3 CD = CO + OD = -+ --= 4. 2 2

Długość ramienia wyliczamy z trójkąta prostokątnego 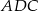ADC .

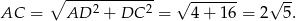
∘ ---2-------2 √ ------- √ -- AC = AD + DC = 4+ 16 = 2 5 .

 
Odpowiedź: √ -- 2 5

Wersja PDF