/Szkoła średnia/Geometria/Planimetria/Trójkąt/Równoramienny

Zadanie nr 7976429

Dodaj do ulubionych
Dodaj do rozwiązanych

Ramię trójkąta równoramiennego jest dwa razy dłuższe od podstawy. Wyznacz obwód trójkąta, jeśli środkowa poprowadzona do ramienia ma długość 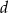d .

Rozwiązanie

Zacznijmy od rysunku i oznaczmy długość podstawy przez a .

PIC

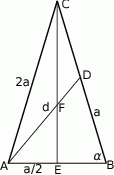
Sposób I

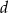To co mamy zrobić, to wyliczyć a w zależności od d . Zauważmy, że ponieważ środkowe dzielą się w stosunku 2:1, jesteśmy w stanie wyliczyć wszystkie boki trójkąta prostokątnego 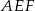AEF . Twierdzenie Pitagorasa zastosowane do tego trójkąta da nam żądaną zależność.

Policzmy najpierw wysokość 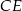CE

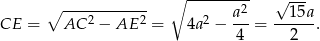
∘ ------------ ∘ -------2- √ --- CE = AC 2 − AE 2 = 4a2 − a--= --15a. 4 2

Stąd

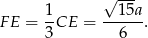
√ --- FE = 1CE = --15a-. 3 6

Piszemy teraz twierdzenie Pitagorasa w trójkącie 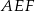AEF .

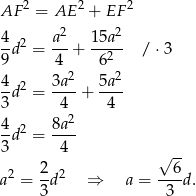
2 2 2 AF = AE + EF 4-2 a2- 15a2- 9d = 4 + 62 / ⋅3 2 2 4d2 = 3a--+ 5a-- 3 4 4 4 8a2 -d2 = ---- 3 4 √ -- 2 2- 2 --6- a = 3d ⇒ a = 3 d.

Zatem obwód jest równy

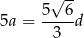
√ -- 5--6- 5a = 3 d

Sposób II

Tym razem skorzystamy z twierdzenia cosinusów. Zanim to jednak zrobimy, popatrzmy na trójkąt prostokątny 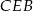CEB .

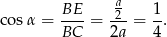
a BE-- 2-- 1- cosα = BC = 2a = 4 .

Piszemy teraz twierdzenie cosinusów w trójkącie 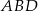ABD .

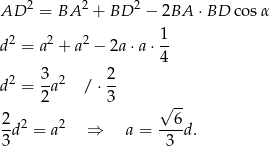
2 2 2 AD = BA + BD − 2BA ⋅BD c osα 2 2 2 1- d = a + a − 2a⋅a ⋅4 3 2 d2 = -a 2 / ⋅-- 2 3 √ -- 2-2 2 --6- 3d = a ⇒ a = 3 d.

Zatem obwód jest równy

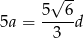
√ -- 5--6- 5a = 3 d

 
Odpowiedź: √ - 5--6d 3

Wersja PDF