Zadanie nr 8237736
Dany jest trójkąt równoramienny 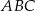 , w którym
, w którym 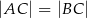 . Na ramieniu
. Na ramieniu 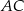 tego trójkąta wybrano punkt
tego trójkąta wybrano punkt 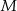 (
(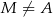 i
i 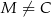 ), a na ramieniu
), a na ramieniu 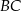 wybrano punkt
wybrano punkt 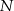 . Przez punkty
. Przez punkty 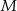 i
i 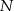 poprowadzono proste prostopadłe do podstawy
poprowadzono proste prostopadłe do podstawy 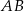 tego trójkąta, które wyznaczają na niej punkty
tego trójkąta, które wyznaczają na niej punkty 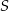 i
i 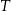 . Wykaż, że jeżeli
. Wykaż, że jeżeli 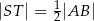 , to
, to 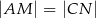 .
.
Rozwiązanie
Szkicujemy opisaną sytuację.
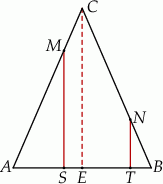
Zauważmy, że trójkąt 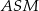 jest podobny do trójkąta
jest podobny do trójkąta 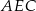 w skali
w skali 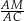 , więc
, więc
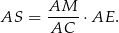
Podobnie, z podobieństwa trójkątów 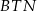 i
i 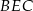 mamy
mamy
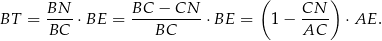
Stąd