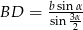/Szkoła średnia/Geometria/Planimetria/Trójkąt/Równoramienny

Zadanie nr 9092733

Dodaj do ulubionych
Dodaj do rozwiązanych

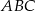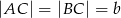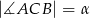W trójkącie równoramiennym ostrokątnym ABC mamy dane |AC | = |BC | = b oraz |∡ACB | = α . Z wierzchołka 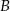B przez środek okręgu opisanego na tym trójkącie poprowadzono prostą, przecinającą bok 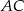AC w punkcie 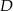D . Oblicz promień okręgu wpisanego w trójkąt 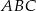ABC oraz długość odcinka BD .

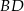Rozwiązanie

Zaczynamy od rysunku.

PIC

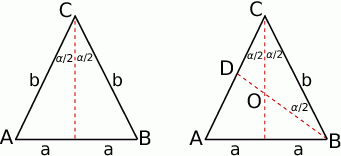
Do wyliczenia promienia okręgu wpisanego w trójkąt informacje o prostej 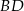BD są zupełnie zbędne – wyliczymy go ze wzoru na pole 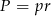P = pr , gdzie 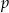p – połowa obwodu. Liczymy

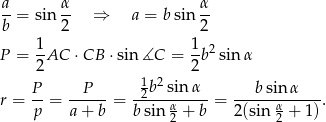
a-= sin α- ⇒ a = bsin α- b 2 2 1 1 2 P = -AC ⋅CB ⋅sin ∡C = -b sin α 2 1 2 2 r = P-= --P---= -2b-sin-α--= --b-sinα----. p a + b bsin α + b 2(sin α + 1) 2 2

Policzmy teraz długość odcinka 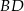BD . Ponieważ środek okręgu opisanego na trójkącie 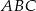ABC jest równo odległy od wierzchołków, trójkąt 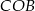COB jest równoramienny, czyli

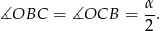
α ∡OBC = ∡OCB = -. 2

Stąd

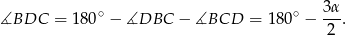
∘ ∘ 3-α ∡BDC = 18 0 − ∡DBC − ∡BCD = 180 − 2 .

Możemy teraz zastosować twierdzenie sinusów do trójkąta 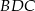BDC .

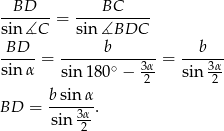
BD BC -------= ----------- sin ∡C sin∡BDC BD---= ------b------ = --b--- sin α sin1 80∘ − 3α sin 3α 2 2 BD = b-sinα-. sin 3α2

 
Odpowiedź: 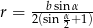r = --bsinα-- 2(sin α2+1) , BD = bsin-α sin 32α

Wersja PDF