/Szkoła średnia/Geometria/Planimetria/Trójkąt/Równoramienny

Zadanie nr 9405361

Dodaj do ulubionych
Dodaj do rozwiązanych

Udowodnij, że w trójkącie równoramiennym środkowe poprowadzone do równych boków są równej długości.

Rozwiązanie

Szkicujemy trójkąt.

PIC

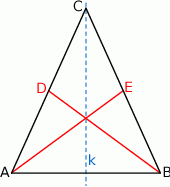
Sposób I

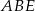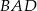Zauważmy, że trójkąty ABE i BAD mają dwa boki tej samej długości: 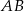AB i

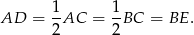
AD = 1AC = 1BC = BE . 2 2

Ponadto kąty między tymi bokami są równe 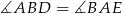∡ABD = ∡BAE , więc trójkąty te są przystające. W szczególności AE = BD .

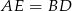Sposób II

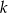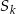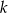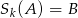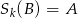Niech k będzie osią symetrii trójkąta i Sk niech oznacza symetrię osiową o osi k . Mamy zatem Sk(A ) = B i Sk(B) = A . Symetria osiowa zachowuje długości odcinków, więc środek 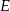E odcinka 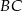BC zostanie w tej symetrii przekształcony na środek 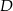D odcinka 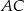AC . To oznacza, że

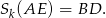
Sk(AE ) = BD .

W szczególności odcinki te mają równe długości.

Wersja PDF