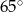/Szkoła średnia/Geometria/Planimetria/Trójkąt/Równoramienny

Zadanie nr 9411876

Ostrokątny trójkąt równoramienny 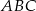ABC o podstawie 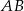AB jest wpisany w okrąg o środku 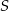S , przy czym kąt 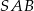SAB ma miarę 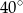4 0∘ . Oblicz miarę kąta CAB .

Wersja PDF

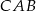Rozwiązanie

Rozpoczynamy od rysunku.

PIC

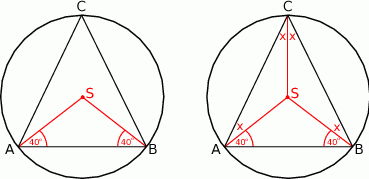
Sposób I

Ponieważ trójkąt 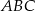ABC jest równoramienny, mamy 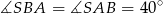∡SBA = ∡SAB = 40 ∘ . W taki razie

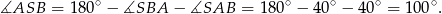
∡ASB = 18 0∘ − ∡SBA − ∡SAB = 18 0∘ − 40∘ − 40∘ = 100 ∘.

Teraz musimy skorzystać z faktu, że kąt wpisany jest połową kąta środkowego opartego na tym samym łuku. Zatem

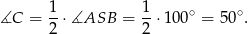
∡C = 1-⋅∡ASB = 1-⋅1 00∘ = 50∘. 2 2

Pozostałe dwa kąty trójkąta są równe, więc każdy z nich musi mieć miarę

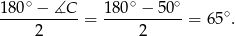
∘ ∘ ∘ 180--−-∡C--= 18-0-−--50- = 65 ∘. 2 2

Sposób II

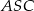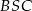Trójkąty ASC i BSC są równoramienne, a ponieważ równoramienny jest też trójkąt 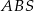ABS , są one przystające. Oznaczmy zatem 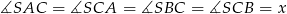∡SAC = ∡SCA = ∡SBC = ∡SCB = x . Suma kątów w trójkącie 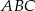ABC jest równa 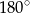180∘ , więc

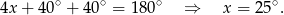
4x+ 40∘ + 40∘ = 1 80∘ ⇒ x = 2 5∘.

zatem 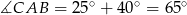∡CAB = 25 ∘ + 4 0∘ = 65∘ .  
Odpowiedź: 65∘

Wersja PDF