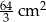/Szkoła średnia/Geometria/Planimetria/Trójkąt/Równoramienny

Zadanie nr 9470376

Dodaj do ulubionych
Dodaj do rozwiązanych

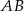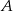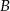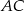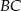W trójkącie równoramiennym podstawa AB ma długość 8 cm. Promień okręgu, stycznego w punktach A i B do prostych zawierających ramiona AC i BC trójkąta, ma długość 5 cm. Oblicz pole trójkąta ABC .

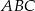Rozwiązanie

Zaczynamy od rysunku.

PIC

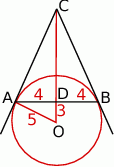
Jeżeli przez 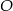O oznaczymy środek okręgu, o którym mowa w treści zadania, to trójkąt 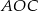AOC jest prostokątny i odcinek 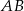AB zawiera jego wysokość opuszczoną z wierzchołka 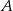A . Z trójkąta prostokątnego 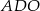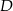ADO (D - środek boku 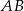AB ) mamy

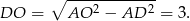
∘ ----2------2- DO = AO − AD = 3.

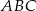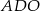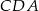Aby obliczyć wysokość trójkąta ABC wykorzystamy podobieństwo trójkątów prostokątnych ADO i CDA (każdy z nich jest podobny do trójkąta prostokątnego 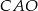CAO ). Mamy zatem

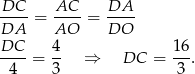
DC--= AC-- = DA-- DA AO DO DC-- 4- 16- 4 = 3 ⇒ DC = 3 .

Zatem pole jest równe

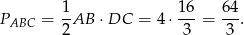
1- 16- 64- PABC = 2AB ⋅DC = 4⋅ 3 = 3 .

 
Odpowiedź: 64 cm 2 3

Wersja PDF