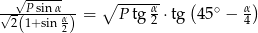/Szkoła średnia/Geometria/Planimetria/Trójkąt/Równoramienny

Zadanie nr 9585757

Dodaj do ulubionych
Dodaj do rozwiązanych

Miara kąta między ramionami trójkąta równoramiennego o polu 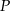P jest równa α . Oblicz promień okręgu wpisanego w ten trójkąt.

Rozwiązanie

Zaczynamy od rysunku.

PIC

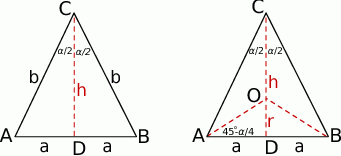
Sposób I

Promień okręgu wpisanego w trójkąt możemy wyliczyć ze wzoru na pole 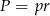P = pr , gdzie 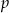p jest połową obwodu. Aby to zrobić musimy wyliczyć obwód. Patrząc na trójkąt prostokątny ADC mamy

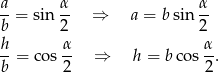
a-= sin α- ⇒ a = b sin α- b 2 2 h α α --= cos -- ⇒ h = bcos -. b 2 2

Korzystając z podanego pola mamy

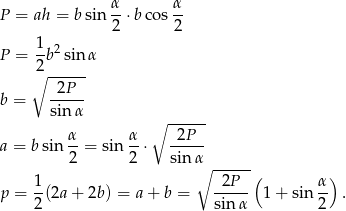
P = ah = b sin α⋅ bcos α- 2 2 1 2 P = --b sinα 2∘ ------ -2P-- b = sin α ∘ ------ a = bsin α-= sin α-⋅ -2P-- 2 2 sin α∘ ------ 1 2P ( α) p = -(2a + 2b ) = a+ b = ----- 1 + sin -- . 2 sin α 2

Liczymy stąd szukany promień

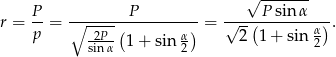
√ ------- P- ---------P-------- -----P-sin-α---- r = p = ∘ -2P-( α) = √ 2(1 + sin α). sin-α 1 + sin 2 2

Sposób II

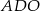Tym razem promień r wyliczymy z trójkąta ADO . Jak poprzednio, najpierw wykorzystamy informację o polu trójkąta

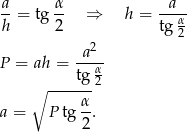
a-= tg α- ⇒ h = -aα- h 2 tg2 a2 P = ah = ---α tg 2 ∘ ----α- a = P tg --. 2

Możemy teraz wyliczyć promień.

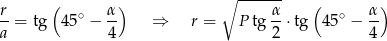
( ) ∘ ------ ( ) -r= tg 45∘ − α- ⇒ r = P tg α⋅ tg 4 5∘ − α- a 4 2 4

 
Odpowiedź: √ ----- ∘ ------ ( ) √---Psin-αα- = P tg α ⋅tg 45∘ − α 2(1+sin 2) 2 4

Wersja PDF