Zadanie nr 9614531
W trójkącie 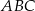 , w którym
, w którym 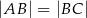 połączono wierzchołek
połączono wierzchołek 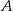 punktem
punktem 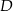 na boku
na boku 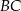 w ten sposób, że
w ten sposób, że 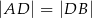 . Wyznacz miary kątów trójkąta
. Wyznacz miary kątów trójkąta 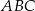 jeżeli
jeżeli 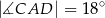 .
.
Rozwiązanie
Rozpoczynamy oczywiście od schematycznego rysunku.
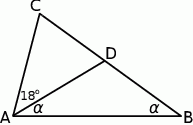
Zauważmy, że z podanych długości odcinków wynika, że trójkąt 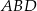 jest równoramienny. Jeżeli więc oznaczymy
jest równoramienny. Jeżeli więc oznaczymy 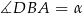 to
to 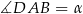 oraz
oraz
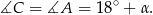
Teraz wystarczy skorzystać z tego, że suma kątów w trójkącie 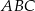 jest równa
jest równa 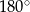 .
.
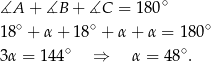
Pozostałe dwa kąty trójkąta 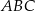 mają więc miary
mają więc miary 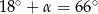 .
.
Odpowiedź: