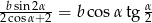/Szkoła średnia/Geometria/Planimetria/Trójkąt/Równoramienny

Zadanie nr 9667841

Dodaj do ulubionych
Dodaj do rozwiązanych

Wyznacz promień okręgu wpisanego w trójkąt równoramienny o ramieniu długości 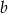b i kącie o mierze α przy podstawie.

Rozwiązanie

Sposób I

Zacznijmy od rysunku.

PIC

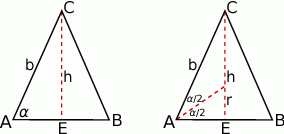
Aby wyliczyć promień okręgu wpisanego w trójkąt 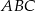ABC będziemy chcieli skorzystać ze wzoru na pole 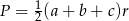P = 12(a+ b+ c)r . Aby to zrobić, najpierw wyliczymy pole i obwód trójkąta ABC .

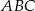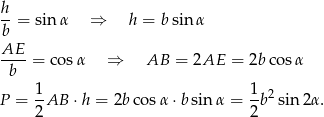
h- b = sin α ⇒ h = bsin α AE ----= cosα ⇒ AB = 2AE = 2b cosα b P = 1AB ⋅h = 2b cos α⋅b sinα = 1b2 sin 2α . 2 2

Mamy zatem

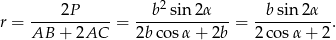
2 r = ----2P----- = --b-sin-2α---= -b-sin2α--. AB + 2AC 2bco sα + 2b 2co sα + 2

Sposób II

Podobnie jak poprzednio zauważmy, że

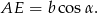
AE = bcos α.

Następnie popatrzmy na trójkąt prostokątny utworzony przez połączenie wierzchołka A ze środkiem okręgu wpisanego (jest to fragment dwusiecznej). Mamy w tym trójkącie

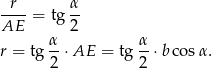
r α AE--= tg 2- α α r = tg --⋅AE = tg--⋅ bcos α. 2 2

 
Odpowiedź: -bsin2α- α 2 cosα+ 2 = bco sα tg 2

Wersja PDF