Zadanie nr 1586493
W trójkącie 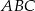 środkowa
środkowa 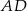 jest prostopadła do boku
jest prostopadła do boku 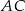 oraz
oraz 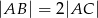 . Oblicz miarę kąta
. Oblicz miarę kąta 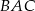 .
.
Rozwiązanie
Rozpoczynamy od rysunku.
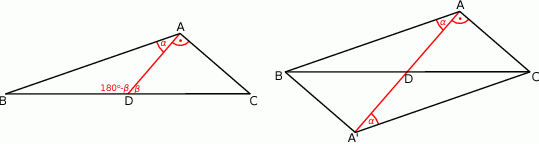
Oznaczmy 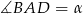 .
.
Sposób I
Niech 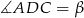 – wtedy
– wtedy 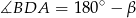 . Piszemy teraz twierdzenia sinusów w trójkątach
. Piszemy teraz twierdzenia sinusów w trójkątach 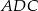 i
i 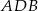 .
.
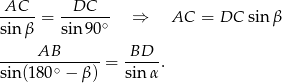
Ponieważ 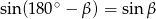 , drugą równość możemy zapisać w postaci
, drugą równość możemy zapisać w postaci
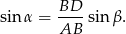
Mamy zatem (korzystamy z pierwszej równości i założenia 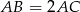 ).
).
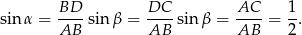
W takim razie 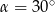 i
i 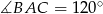 .
.
Sposób II
Zauważmy, że trójkąty 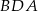 i
i 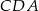 mają równe pola (bo mają wspólną wysokość opuszczoną z wierzchołka
mają równe pola (bo mają wspólną wysokość opuszczoną z wierzchołka 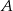 i podstawy tej samej długości). Na mocy wzoru na pole trójkąta z sinusem mamy
i podstawy tej samej długości). Na mocy wzoru na pole trójkąta z sinusem mamy
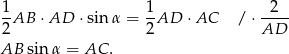
Korzystamy teraz z równości 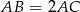 .
.
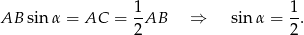
Zauważmy jeszcze, że kąt 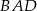 musi być ostry, bo łącznie z kątem
musi być ostry, bo łącznie z kątem 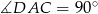 tworzy kąt trójkąta. Mamy zatem
tworzy kąt trójkąta. Mamy zatem 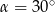 oraz
oraz
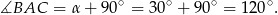
Sposób III
Niech 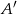 będzie odbiciem punktu
będzie odbiciem punktu 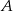 względem punktu
względem punktu 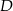 . Otrzymujemy w ten sposób równoległobok
. Otrzymujemy w ten sposób równoległobok 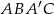 , w którym
, w którym 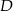 jest punktem przecięcia się przekątnych. Zauważmy, że trójkąt
jest punktem przecięcia się przekątnych. Zauważmy, że trójkąt 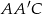 jest prostokątny oraz
jest prostokątny oraz
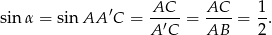
Zatem 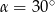 i
i 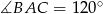 .
.
Sposób IV
Tym razem dorysujmy wysokość 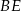 opuszczoną z wierzchołka
opuszczoną z wierzchołka 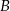 na bok
na bok 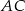 .
.
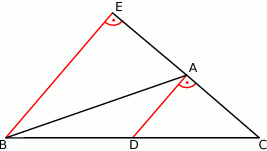
Na mocy twierdzenia Talesa mamy
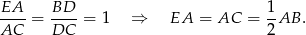
To oznacza, że trójkąt prostokątny 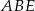 jest połówką trójkąta równobocznego. W szczególności
jest połówką trójkąta równobocznego. W szczególności 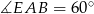 i
i
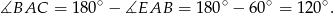
Odpowiedź: