/Szkoła średnia/Geometria/Planimetria/Trójkąt/Dowolny/Kąty

Zadanie nr 1756024

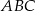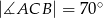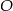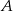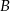W trójkącie ABC , w którym ∘ |∡ACB | = 70 połączono środek okręgu wpisanego O z wierzchołkami A i B . Oblicz miarę kąta AOB .

PIC

Wersja PDF

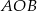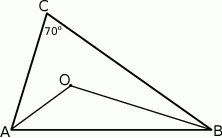
Rozwiązanie

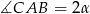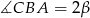Oznaczmy ∡CAB = 2 α i ∡CBA = 2β .

PIC

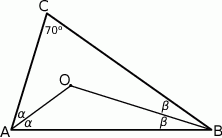
W takim razie

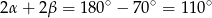
2 α+ 2β = 18 0∘ − 70∘ = 110∘

(bo suma kątów w trójkącie 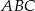ABC jest równa 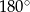180∘ ), czyli α+ β = 55 ∘ .

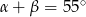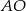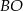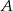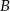Ponieważ proste AO i BO są dwusiecznymi kątów przy wierzchołkach A i B , z trójkąta 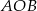AOB mamy

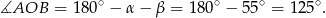
∘ ∘ ∘ ∘ ∡AOB = 180 − α − β = 1 80 − 55 = 12 5 .

 
Odpowiedź: 125 ∘

Wersja PDF