/Szkoła średnia/Geometria/Planimetria/Trójkąt/Dowolny/Kąty

Zadanie nr 3478104

Boki trójkąta mają długości 4, 8 i 10.

  • Oblicz cosinus i tangens kąta leżącego naprzeciwko najkrótszego boku.
  • Oblicz długość środkowej poprowadzonej do najdłuższego boku.
Wersja PDF

Rozwiązanie

PIC

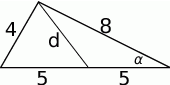
  • Szukany cosinus obliczymy z twierdzenia cosinusów.
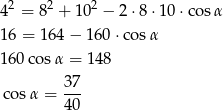
    42 = 82 + 1 02 − 2⋅8 ⋅10 ⋅cos α 16 = 164 − 160 ⋅cos α 16 0cos α = 148 37 cosα = --- 40

    Tangens policzymy korzystając z tego, że sinus jest dodatni dla kątów trójkąta (w przedziale (0,π ) ).

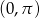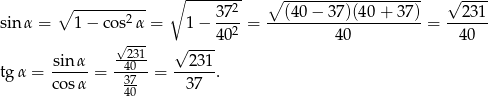
    ∘ -------- ∘ ---------- 372 ∘ (40-−-37-)(4-0+--37) √ 2-31 sin α = 1 − co s2α = 1− --2-= ----------------------= ------ √ --- √ ----40 40 40 sin α --231- 231 tg α = ----- = -4307--= ------. co sα 40 37

     
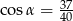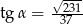
    Odpowiedź: cosα = 3470 , √-231 tg α = 37

  • Długość środkowej liczymy z twierdzenia cosinusów.
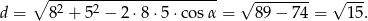
    ∘ ----------------------- √ -------- √ --- d = 82 + 52 − 2 ⋅8⋅5 ⋅cos α = 89 − 74 = 15.

     
    Odpowiedź: √ --- 15

Wersja PDF