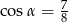Zadanie nr 4618852
Dany jest trójkąt o bokach długości 1, 
, 2. Oblicz cosinus i sinus kąta leżącego naprzeciw najkrótszego boku tego trójkąta.
Rozwiązanie
Zacznijmy od rysunku.
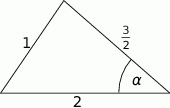
Aby wyliczyć cosinus kąta 
korzystamy z twierdzenia cosinusów:
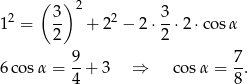
Wartość funkcji sinus wyliczymy z jedynki trygonometrycznej:
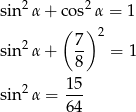
Ponieważ 
jest kątem ostrym (bo cosinus jest dodatni) to otrzymujemy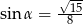 
.
Odpowiedź: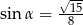 
, 
