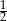Zadanie nr 4658470
Kąty 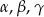 trójkąta
trójkąta 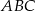 spełniają zależność
spełniają zależność
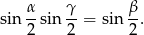
Oblicz wartość wyrażenia 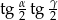 .
.
Rozwiązanie
Ponieważ 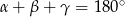 , daną równość możemy przekształcić następująco.
, daną równość możemy przekształcić następująco.
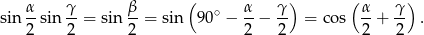
Korzystamy teraz ze wzoru na cosinus sumy.
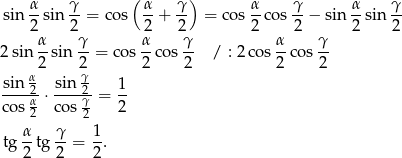
Odpowiedź: 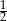
 Największy internetowy zbiór zadań z matematyki
Największy internetowy zbiór zadań z matematyki
Kąty 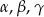 trójkąta
trójkąta 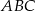 spełniają zależność
spełniają zależność
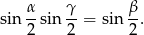
Oblicz wartość wyrażenia 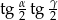 .
.
Ponieważ 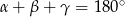 , daną równość możemy przekształcić następująco.
, daną równość możemy przekształcić następująco.
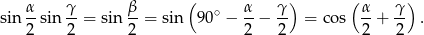
Korzystamy teraz ze wzoru na cosinus sumy.
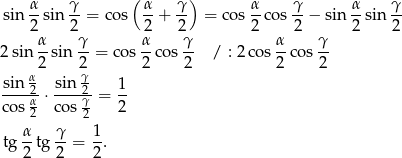
Odpowiedź: