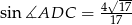Zadanie nr 4869024
W trójkącie 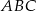 , w którym
, w którym 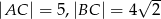 i
i 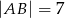 na boku
na boku 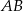 wybrano taki punkt
wybrano taki punkt 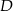 , że
, że 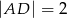 . Oblicz sinus kąta
. Oblicz sinus kąta 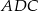 .
.
Rozwiązanie
Rozpoczynamy od szkicowego rysunku.
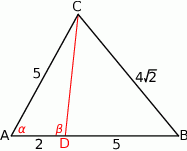
Sinus kąta 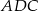 możemy wyliczyć korzystając z twierdzenia sinusów lub cosinusów w trójkącie
możemy wyliczyć korzystając z twierdzenia sinusów lub cosinusów w trójkącie 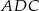 , ale zanim to zrobimy musimy obliczyć długość odcinka
, ale zanim to zrobimy musimy obliczyć długość odcinka 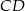 . Możemy obliczyć tę długość pisząc twierdzenie cosinusów w trójkącie
. Możemy obliczyć tę długość pisząc twierdzenie cosinusów w trójkącie 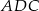 – do tego potrzebujemy
– do tego potrzebujemy 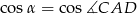 .
.
Liczymy. Piszemy twierdzenie cosinusów w trójkącie 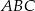 .
.
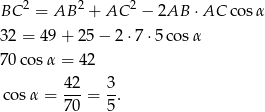
Teraz stosujemy twierdzenie cosinusów w trójkącie 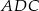 .
.
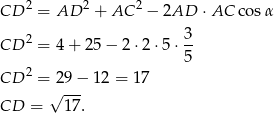
Interesujący nas 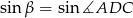 obliczymy na dwa sposoby.
obliczymy na dwa sposoby.
Sposób I
Chcemy skorzystać z twierdzenia sinusów w trójkącie 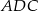 . Najpierw obliczmy jednak
. Najpierw obliczmy jednak 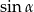 .
.
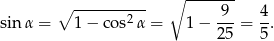
Teraz piszemy twierdzenie sinusów w trójkącie 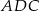 .
.
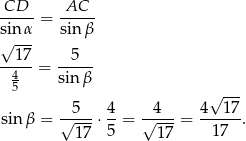
Sposób II
Tym razem skorzystamy z twierdzenia cosinusów. Piszemy twierdzenie cosinusów w trójkącie 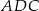 .
.
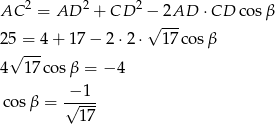
Pozostało skorzystać z jedynki trygonometrycznej.
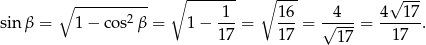
Odpowiedź: