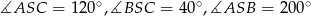Zadanie nr 4894656
W trójkącie 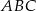 mamy dane
mamy dane 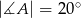 oraz
oraz 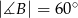 . Punkt
. Punkt 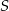 jest środkiem okręgu opisanego na tym trójkącie. Oblicz miary kątów
jest środkiem okręgu opisanego na tym trójkącie. Oblicz miary kątów 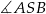 ,
, 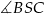 i
i 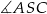 .
.
Rozwiązanie
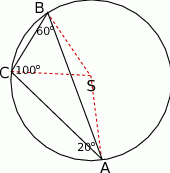
Jeżeli dorysujemy okrąg opisany na trójkącie  (trójkąt jest rozwartokątny, więc środek okręgu jest na zewnątrz trójkąta), to ponieważ kąt środkowy jest dwa razy większy od kąta wpisanego opartego na tym samym łuku, mamy
(trójkąt jest rozwartokątny, więc środek okręgu jest na zewnątrz trójkąta), to ponieważ kąt środkowy jest dwa razy większy od kąta wpisanego opartego na tym samym łuku, mamy
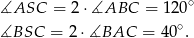
Ponadto
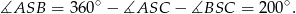
Odpowiedź: