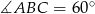/Szkoła średnia/Geometria/Planimetria/Trójkąt/Dowolny/Kąty

Zadanie nr 6541351

Wysokość 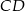CD trójkąta 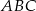ABC ma długość 6cm i dzieli bok 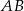AB na odcinki o długościach 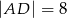|AD | = 8 i √ -- |BD | = 2 3 .

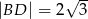  • Oblicz tangens i cosinus kąta ∡BAC .
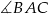  • Znajdź miarę kąta ∡ABC .
Wersja PDF

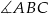Rozwiązanie

Zacznijmy od rysunku

PIC

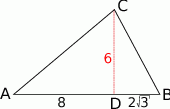
Policzmy na początku (z twierdzenia Pitagorasa) długość boku 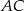AC .

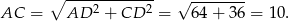
∘ ------------ √ -------- AC = AD 2 + CD 2 = 64 + 3 6 = 10.

Teraz policzmy żądane wartości funkcji trygonometrycznych

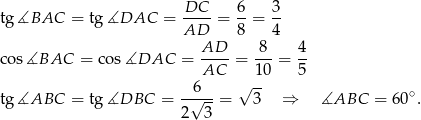
tg ∡BAC = tg ∡DAC = -DC- = 6-= 3- AD 8 4 AD-- -8- 4- co s∡BAC = cos∡DAC = AC = 10 = 5 6 √ -- tg ∡ABC = tg ∡DBC = -√---= 3 ⇒ ∡ABC = 60∘. 2 3

 
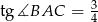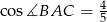Odpowiedź: tg ∡BAC = 34 , cos∡BAC = 45 , ∡ABC = 60∘

Wersja PDF